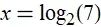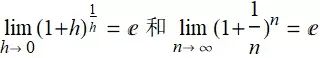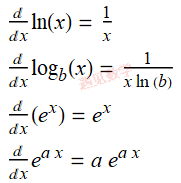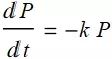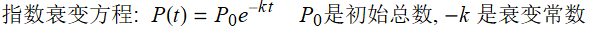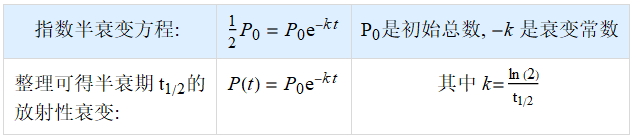【指数函数和对数函数】图解普林斯顿微积分 08

第 9 章指数函数和对数函数

本章的主要内容:

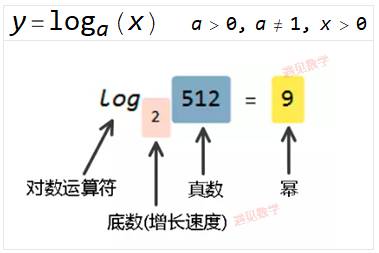
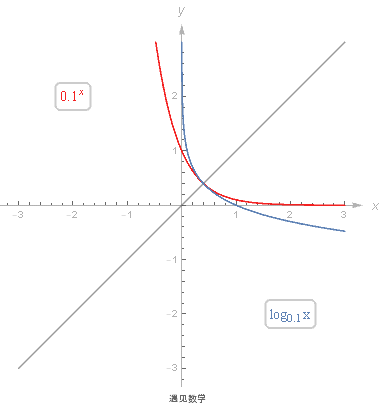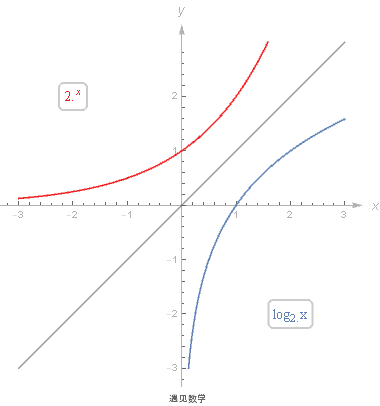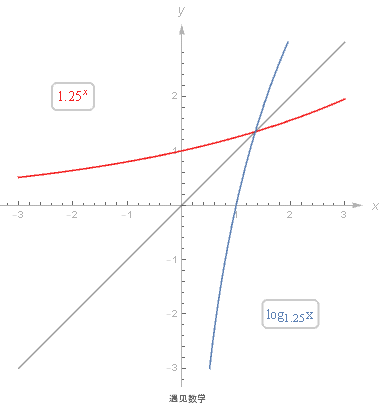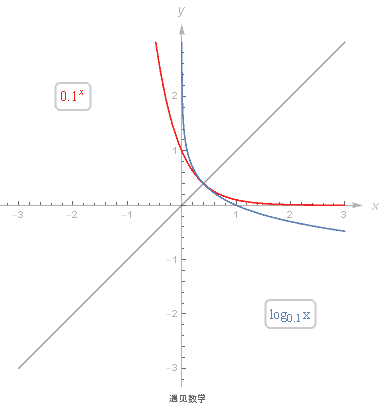
• 回顾指数函数和对数函数的基本知识, 以及两者是如何相互关联的;

• e 的定义和性质;

• 如何对指数函数和对数函数求导;

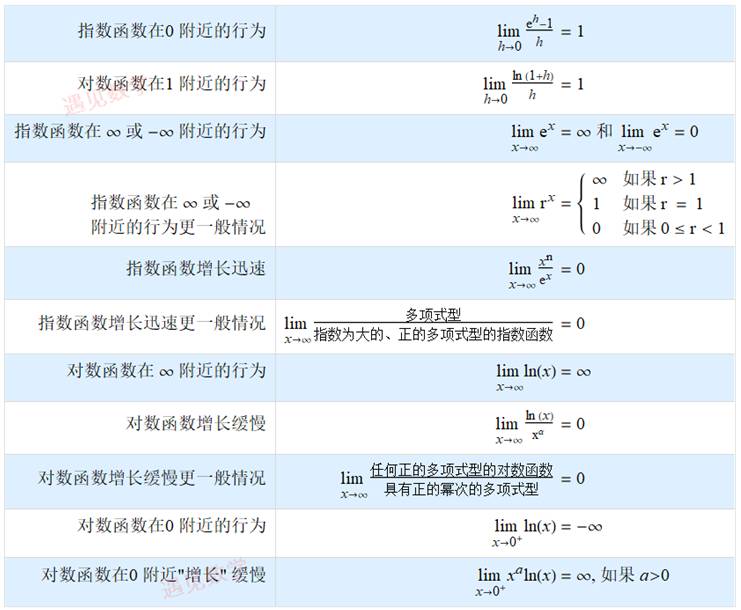
• 如何求解涉及指数函数和对数函数的极限问题;

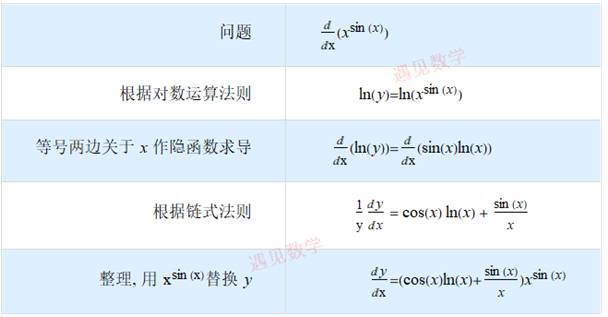
• 对数函数的微分;

• 指数增长和指数衰变;

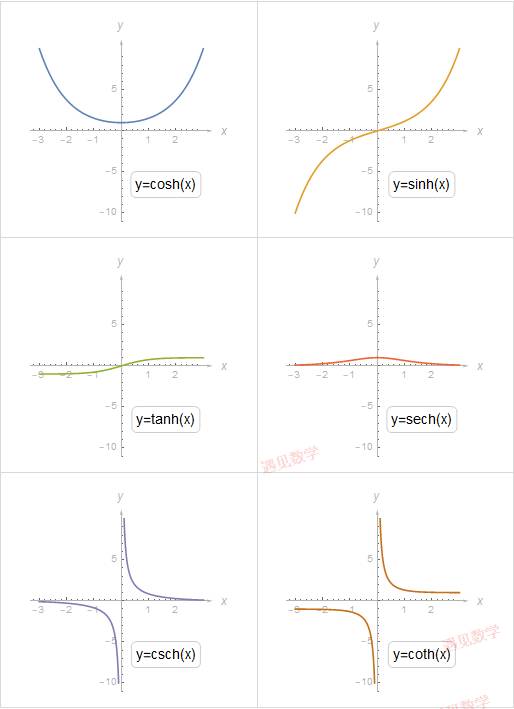
• 双曲函数.

9.1 基础知识

首先需要掌握三点:指数运算法则、对数和指数的关系, 以及对数运算法则.

9.1.1 指数函数的回顾

例如, 数 $2^{-5/2}$ 是一个底数为 2, 指数为 -5/2 的幂. 指数运算法则告诉我们指数函数如何运算的:

至于指数函数的图像, 可以查看第一章的内容, 跳转链接.

9.1.2 对数函数的回顾

对数(Logarithms), 比如想要求解 $2^x\text{=7}$ 中的 x , 需要对方程两边取对数. 由于左边的底数是 2, 对数的底就是 2. 于是方程的解就是:

符号解释:

9.1.3 对数函数、指数函数及反函数

关注两者的关系, 请直接看下面的动图图片吧.

9.1.4 对数运算法则

9.2 e 的定义

9.2.1 一个有关复利的问题

更详细内容请查看《自然常数 E 的故事》文章中的内容, 跳转链接>>>.

注意: 因为以 e 为底的对数是如此常见, 所以经常会用 ln(x) , 而不是 ${\log }_e\text{(x)}$来表示(读 x 的自然对数). 底数为 e 的对数称为自然对数.

9.3 对数函数和指数函数求导

9.4 求解指数函数或对数函数的极限

9.5 取对数求导法

取对数求导法是一个有用的技巧, 可以处理这样 $\text{f(x}{)}^{g\left(x\right)}$ 这样底数和指数均为 x 的函数的导数问题. 下面的例子:

9.6 指数增长和指数衰变(Exponential Growth and Decay)

自然界中某些情况下, 动物种群的总数会呈现指数增长, 还有物质会有指数衰变, 如放射性衰变可以帮助来确定物质的年龄.

9.6.1 指数增长

假设有一个种群以指数增长. 用符号表示, 设 P 是在时刻 t 时的总数, 并设 k 是增长常数. P 的微分方程为:

9.6.2 指数衰变

自然界中有些元素的原子具有放射性, 一段时间后, 原子核分裂, 它们变成别的元素, 同时释放出能量.

这里的 k 是常数, 也就是说 P 的变化率是 P 的负倍数.

还有数量减半的时间长度被称为原子的半衰期(half-life).

9.7 双曲函数

双曲函数是伪装的指数函数, 并且在很多方面又和三角函数非常相似.

除了 cosh(x) 双曲余弦函数和 sech(x) 双曲正割函数是偶函数外, 所有的双曲三)角函数都是奇函数. 这和原来常规的三角函数的情况相同!(本章完)

「予人玫瑰, 手留余香」

转发既是支持和帮助, 感谢感谢!