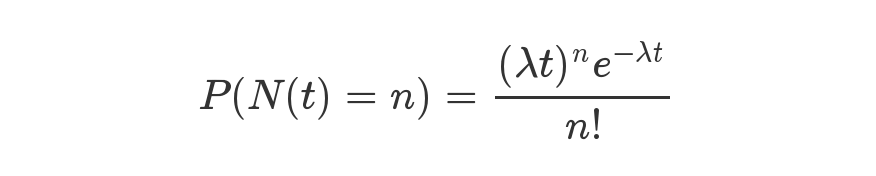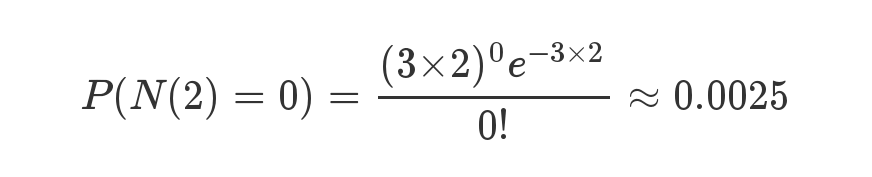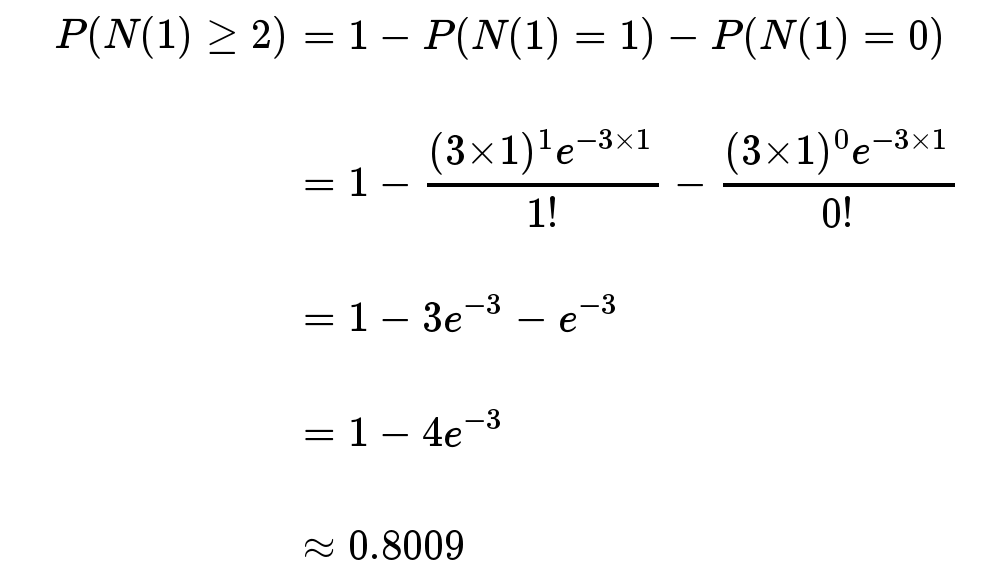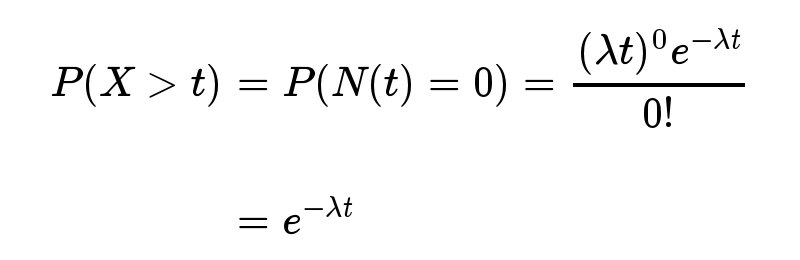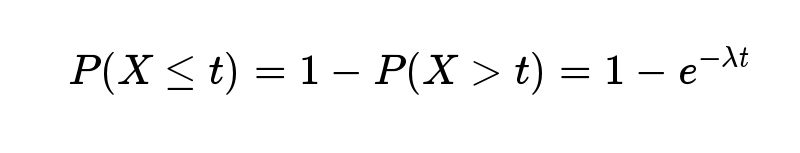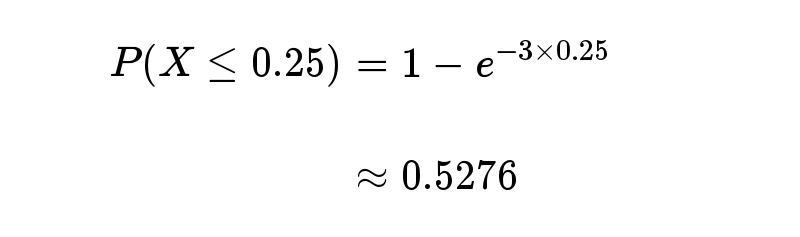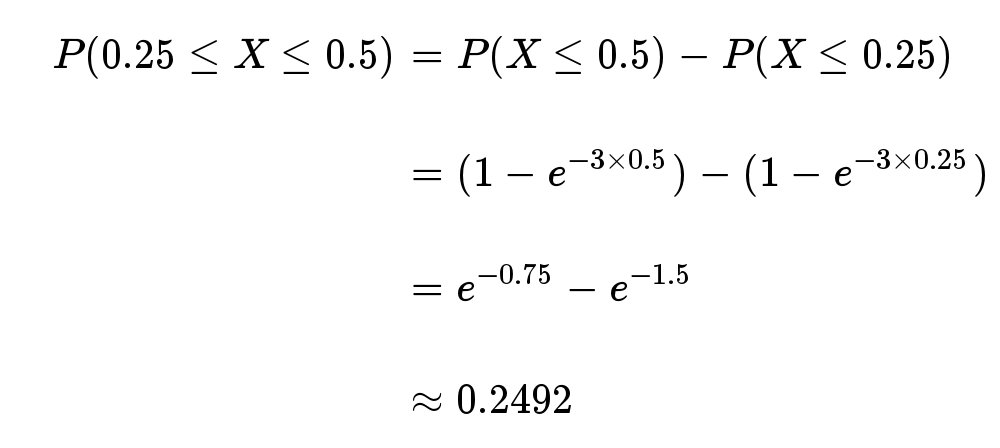泊松分布和指数分布：10分钟教程

转自: http://www.ruanyifeng.com/blog/2015/06/poisson-distribution.html

大学时，我一直觉得统计学很难，还差点挂科。

工作以后才发现，难的不是统计学，而是我们的教材写得不好。比起高等数学，统计概念其实容易理解多了。

我举一个例子，什么是泊松分布和指数分布？恐怕大多数人都说不清楚。

我可以在10分钟内，让你毫不费力地理解这两个概念。

01

—

泊松分布

日常生活中，大量事件是有固定频率的。

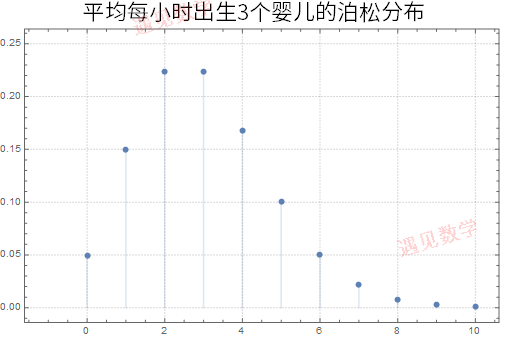
• 某医院平均每小时出生3个婴儿

• 某公司平均每10分钟接到1个电话

• 某超市平均每天销售4包xx牌奶粉

• 某网站平均每分钟有2次访问

它们的特点就是，我们可以预估这些事件的总数，但是没法知道具体的发生时间。已知平均每小时出生3个婴儿，请问下一个小时，会出生几个？

有可能一下子出生6个，也有可能一个都不出生。这是我们没法知道的。

泊松分布就是描述某段时间内，事件具体的发生概率。

上面就是泊松分布的公式。等号的左边，P 表示概率，N表示某种函数关系，t 表示时间，n 表示数量，1小时内出生3个婴儿的概率，就表示为 P(N(1) = 3) 。等号的右边，λ 表示事件的频率。

接下来两个小时，一个婴儿都不出生的概率是0.25%，基本不可能发生。

接下来一个小时，至少出生两个婴儿的概率是80%。

泊松分布的图形大概是下面的样子。

可以看到，在频率附近，事件的发生概率最高，然后向两边对称下降，即变得越大和越小都不太可能。每小时出生3个婴儿，这是最可能的结果，出生得越多或越少，就越不可能。

02

—

指数分布

指数分布是事件的时间间隔的概率。下面这些都属于指数分布。

• 婴儿出生的时间间隔

• 来电的时间间隔

• 奶粉销售的时间间隔

• 网站访问的时间间隔

指数分布的公式可以从泊松分布推断出来。如果下一个婴儿要间隔时间 t ，就等同于 t 之内没有任何婴儿出生。

反过来，事件在时间 t 之内发生的概率，就是1减去上面的值。

接下来15分钟，会有婴儿出生的概率是52.76%。

接下来的15分钟到30分钟，会有婴儿出生的概率是24.92%。

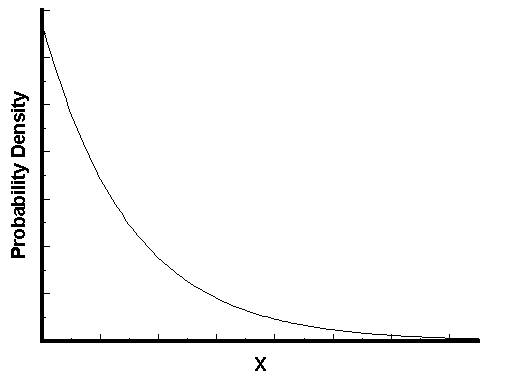
指数分布的图形大概是下面的样子。

可以看到，随着间隔时间变长，事件的发生概率急剧下降，呈指数式衰减。想一想，如果每小时平均出生3个婴儿，上面已经算过了，下一个婴儿间隔2小时才出生的概率是0.25%，那么间隔3小时、间隔4小时的概率，是不是更接近于0？

03

—

总结

一句话总结：泊松分布是单位时间内独立事件发生次数的概率分布，指数分布是独立事件的时间间隔的概率分布。

请注意是"独立事件"，泊松分布和指数分布的前提是，事件之间不能有关联，否则就不能运用上面的公式。

[说明] 本文受到 nbviewer 文档的启发。

（正文完） 

「予人玫瑰, 手留余香」

转发既是支持帮助[遇见数学]更快发展, 非常感谢!