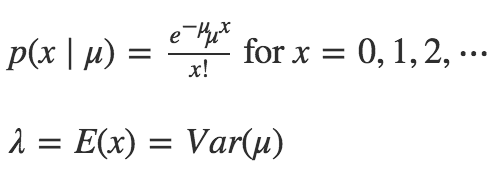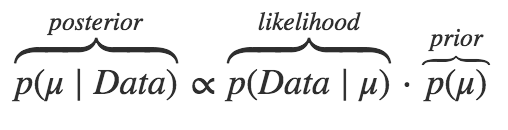用 Python 进行贝叶斯模型建模（1）

（点击上方蓝字，快速关注我们）

编译：伯乐在线 - JLee

如有好文章投稿，请点击 → 这里了解详情

本系列：

• 《第 0 节：导论》

• 《第 1 节：估计模型参数》

第1节：估计模型参数

在这一节，我们将讨论贝叶斯方法是如何思考数据的，我们怎样通过 MCMC 技术估计模型参数。

from IPython.display import Image

 

import matplotlib.pyplot as plt

import numpy as np

import pandas as pd

import pymc3 as pm

import scipy

import scipy.stats as stats

import scipy.optimize as opt

import statsmodels.api as sm

 

%matplotlib inline

 

plt.style.use('bmh')

colors = ['#348ABD', '#A60628', '#7A68A6', '#467821', '#D55E00',

          '#CC79A7', '#56B4E9', '#009E73', '#F0E442', '#0072B2']

 

messages = pd.read_csv('data/hangout_chat_data.csv')

贝叶斯方法如何思考数据？

当我开始学习如何运用贝叶斯方法的时候，我发现理解贝叶斯方法如何思考数据是很有用的。设想下述的场景：

一个好奇的男孩每天观察从他家门前经过的汽车的数量。他每天努力地记录汽车的总数。一个星期过去后，他的笔记本上记录着下面的数字：12,33,20,29,20,30,18

从贝叶斯方法的角度看，这个数据是由随机过程产生的。但是，既然数据被观测，它便固定了并且不会改变。这个随机过程有些模型参数被固定了。然而，贝叶斯方法用概率分布来表示这些模型参数的不确定性。

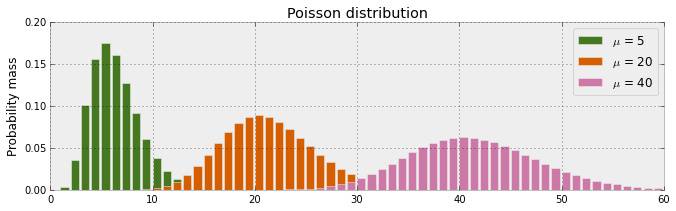
由于这个男孩调查的是计数（非负整数），一个通常的做法是用泊松分布对数据（如随机过程）建模。泊松分布只有一个参数 μ，它既是数据的平均数，也是方差。下面是三个不同 μ 值的泊松分布。

代码：

fig = plt.figure(figsize=(11,3))

ax = fig.add_subplot(111)

x_lim = 60

mu = [5, 20, 40]

for i in np.arange(x_lim):

    plt.bar(i, stats.poisson.pmf(mu[0], i), color=colors[3])

    plt.bar(i, stats.poisson.pmf(mu[1], i), color=colors[4])

    plt.bar(i, stats.poisson.pmf(mu[2], i), color=colors[5])

    

_ = ax.set_xlim(0, x_lim)

_ = ax.set_ylim(0, 0.2)

_ = ax.set_ylabel('Probability mass')

_ = ax.set_title('Poisson distribution')

_ = plt.legend(['$mu$ = %s' % mu[0], '$mu$ = %s' % mu[1], '$mu$ = %s' % mu[2]])

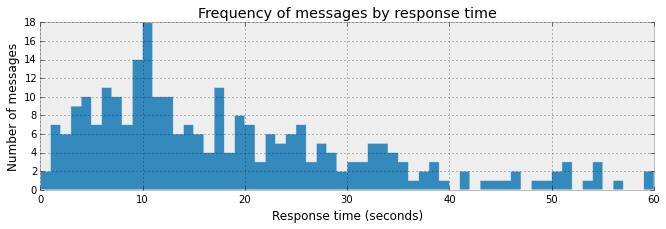
在上一节中，我们引入我的 hangout 聊天数据集。特别地，我对我的回复时间（response_time）感兴趣。鉴于 response_time 是计数数据，我们可以用泊松分布对其建模，并估计参数 μ 。我们将用频率论方法和贝叶斯方法两种方法来估计。

fig = plt.figure(figsize=(11,3))

_ = plt.title('Frequency of messages by response time')

_ = plt.xlabel('Response time (seconds)')

_ = plt.ylabel('Number of messages')

_ = plt.hist(messages['time_delay_seconds'].values,

             range=[0, 60], bins=60, histtype='stepfilled')

频率论方法估计μ

在进入贝叶斯方法之前，让我们先看一下频率论方法估计泊松分布参数。我们将使用优化技术使似然函数最大。

下面的函数poisson_logprob()返回在给定泊松分布模型和参数值的条件下，观测数据总体的可能性。用方法opt.minimize_scalar找到在观测数据基础上参数值 μ 的最可信值（最大似然）。该方法的机理是，这个优化技术会自动迭代可能的mu值直到找到可能性最大的值。

y_obs = messages['time_delay_seconds'].values

 

def poisson_logprob(mu, sign=-1):

    return np.sum(sign*stats.poisson.logpmf(y_obs, mu=mu))

 

freq_results = opt.minimize_scalar(poisson_logprob)

%time print("The estimated value of mu is: %s" % freq_results['x'])

The estimated value of mu is: 18.0413533867

CPU times: user 63 µs, sys: 1e+03 ns, total: 64 µs

Wall time: 67.9 µs

所以，μ 的估计值是18.0413533867。优化技术没有对不确定度进行评估，它只返回一个点，效率很高。

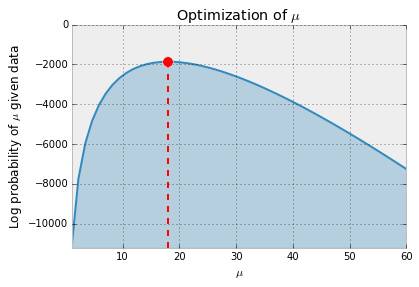
下图描述的是我们优化的函数。对于每个μ值，图线显示给定数据和模型在μ处的似然度。优化器以登山模式工作——从曲线上随机一点开始，不停向上攀登直到达到最高点。

x = np.linspace(1, 60)

y_min = np.min([poisson_logprob(i, sign=1) for i in x])

y_max = np.max([poisson_logprob(i, sign=1) for i in x])

fig = plt.figure(figsize=(6,4))

_ = plt.plot(x, [poisson_logprob(i, sign=1) for i in x])

_ = plt.fill_between(x, [poisson_logprob(i, sign=1) for i in x],

                     y_min, color=colors[0], alpha=0.3)

_ = plt.title('Optimization of $mu$')

_ = plt.xlabel('$mu$')

_ = plt.ylabel('Log probability of $mu$ given data')

_ = plt.vlines(freq_results['x'], y_max, y_min, colors='red', linestyles='dashed')

_ = plt.scatter(freq_results['x'], y_max, s=110, c='red', zorder=3)

_ = plt.ylim(ymin=y_min, ymax=0)

_ = plt.xlim(xmin=1, xmax=60)

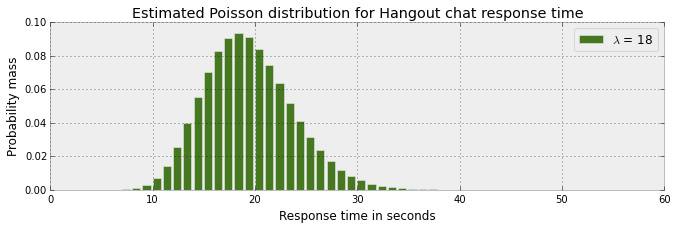
上述优化方法估计泊松分布的参数值为  18 .我们知道，对任意一个泊松分布，参数 μ 代表的是均值和方差。下图描述了这个分布。

fig = plt.figure(figsize=(11,3))

ax = fig.add_subplot(111)

x_lim = 60

mu = np.int(freq_results['x'])

for i in np.arange(x_lim):

    plt.bar(i, stats.poisson.pmf(mu, i), color=colors[3])

    

_ = ax.set_xlim(0, x_lim)

_ = ax.set_ylim(0, 0.1)

_ = ax.set_xlabel('Response time in seconds')

_ = ax.set_ylabel('Probability mass')

_ = ax.set_title('Estimated Poisson distribution for Hangout chat response time')

_ = plt.legend(['$lambda$ = %s' % mu])

上述泊松分布模型和 μ 的估计表明，观测小于10 或大于 30 的可能性很小，绝大多数的概率分布在 10 和 30 之间。但是，这不能反映我们观测到的介于 0 到 60 之间的数据。

贝叶斯方法估计 μ

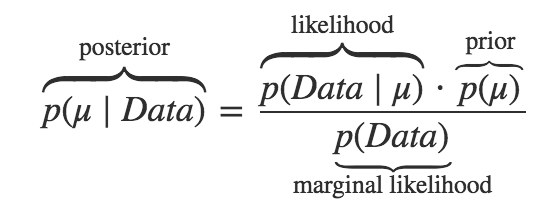
如果你之前遇到过贝叶斯理论，下面的公式会看起来很熟悉。我从没认同过这个框架直到我读了John K. Kruschke的书“贝叶斯数据分析”，从他优美简洁的贝叶斯图表模型视角认识这个公式。

代码：

Image('graphics/Poisson-dag.png', width=320)

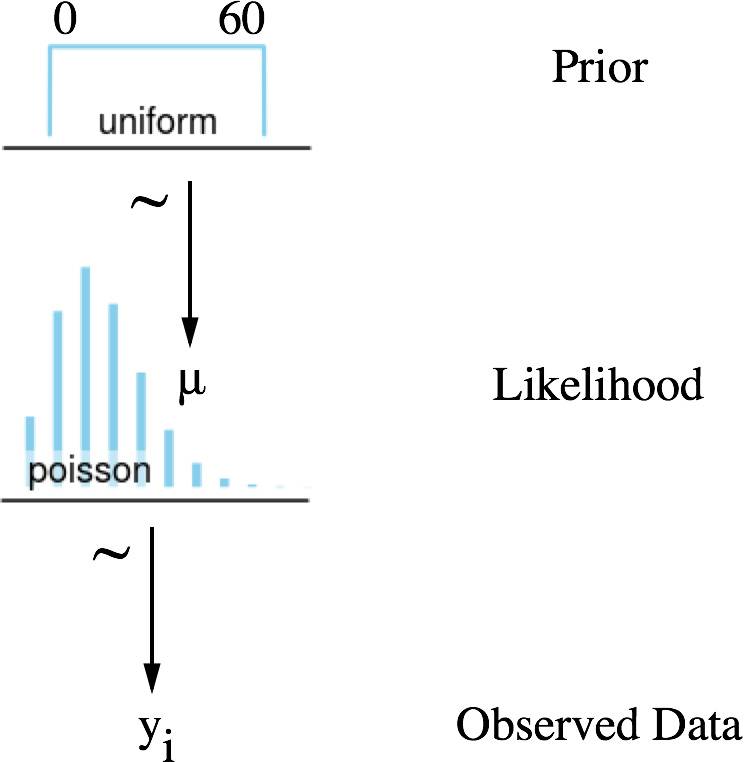
上述模式可以解读如下（从下到上）：

• 对每一个对话（i）观测计数数据（y）

• 数据由一个随机过程产生，我们认为可以用泊松分布模拟

• 泊松分布只有一个参数，介于 0 到 60 之间

由于我们没有任何依据对μ在这个范围内进行预估，就用均匀分布对 μ 建模

神奇的方法MCMC

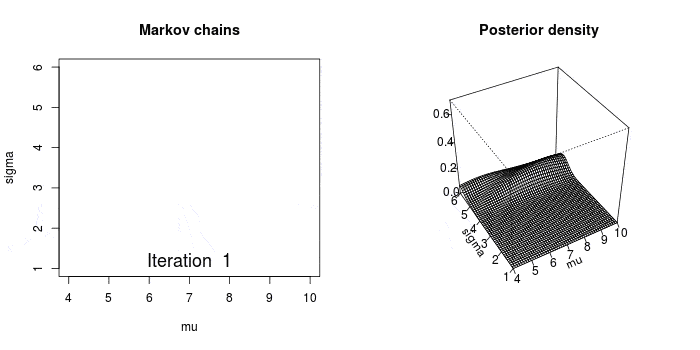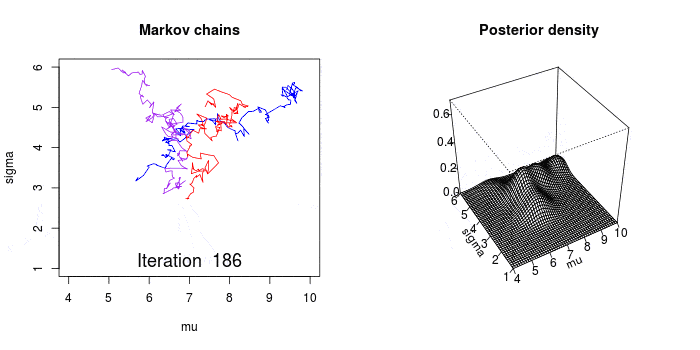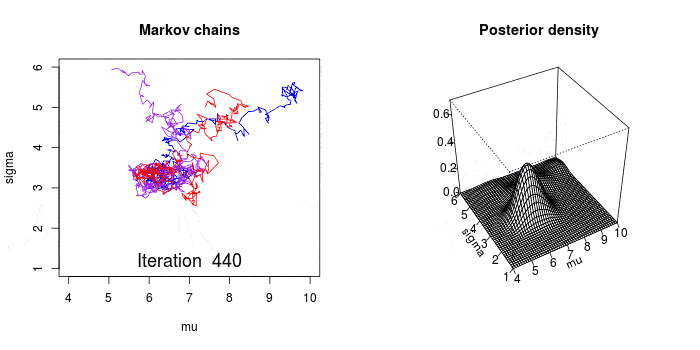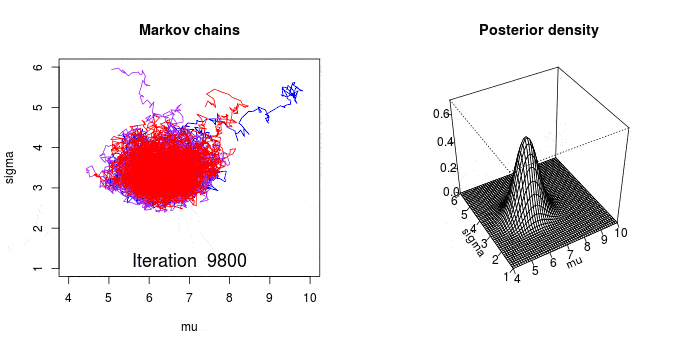
下面的动画很好的演示了马尔科夫链蒙特卡罗方法（MCMC）的过程。MCMC采样器从先验分布中选取参数值，计算从这些参数值决定的某个分布中得到观测数据的可能性。

这个计算可以作为MCMC采样器的导引。从参数的先验分布中选取值，然后计算给定数据条件下这些参数值可能性——导引采样器到更高概率的区域。

与上面讨论的频率论优化技术在概念上有相似之处，MCMC采样器向可能性最高的区域运动。但是，贝叶斯方法不关心寻找绝对最大值，而是遍历和收集概率最高区域附近的样本。所有收集到的样本都可认为是一个可信的参数。

Image(url='graphics/mcmc-animate.gif')

with pm.Model() as model:

    mu = pm.Uniform('mu', lower=0, upper=60)

    likelihood = pm.Poisson('likelihood', mu=mu, observed=messages['time_delay_seconds'].values)

    

    start = pm.find_MAP()

    step = pm.Metropolis()

    trace = pm.sample(200000, step, start=start, progressbar=True)

Applied interval-transform to mu and added transformed mu_interval to model.

[-----------------100%-----------------] 200000 of 200000 complete in 48.3 sec

上面的代码通过遍历 μ 的后验分布的高概率区域，收集了 200,000 个 μ 的可信样本。下图（左）显示这些值的分布，平均值与频率论的估值（红线）几乎一样。但是，我们同时也得到了不确定度，μ 值介于 17 到 19 之间都是可信的。我们稍后会看到这个不确定度很有价值。

_ = pm.traceplot(trace, varnames=['mu'], lines={'mu': freq_results['x']})

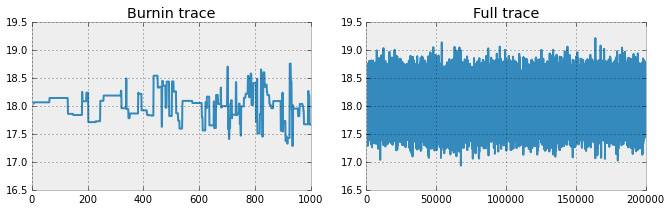
丢弃早期样本（坏点）

你可能疑惑上面 MCMC 代码中pm.find.MAP()的作用。MAP 代表最大后验估计，它帮助 MCMC 采样器寻找合适的采样起始点。理想情况下，模型从高概率区域开始，但有时不是这样。因此，样本集中的早期样本（坏点）经常被丢弃。

fig = plt.figure(figsize=(11,3))

plt.subplot(121)

_ = plt.title('Burnin trace')

_ = plt.ylim(ymin=16.5, ymax=19.5)

_ = plt.plot(trace.get_values('mu')[:1000])

fig = plt.subplot(122)

_ = plt.title('Full trace')

_ = plt.ylim(ymin=16.5, ymax=19.5)

_ = plt.plot(trace.get_values('mu'))

模型的收敛性

样本轨迹

由于上面模型对 μ 的估计不能表明估计的效果很好,可以采用一些检验手段。首先，观察样本输出，样本的轨迹应该轻微上下浮动，就像一条毛虫。如果你看到轨迹上下跳跃或滞留在某点，这就是模型不收敛的标志，通过 MCMC 采样器得到的估计没有意义。

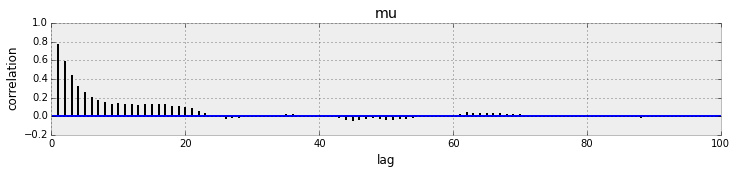
自相关图

也可采另一种测试，自相关测试（见下图），这是评估MCMC采样链中样本前后相关关系的一种方法。相关性弱的样本比相关性强的样本能够给参数估计提供更多的信息。

直观上看，自相关图应该快速衰减到0附近，然后在 0 附近上下波动。如果你的自相关图没有衰减，通常这是弱融合的标志，你需要重新审查你的模型选择（如似然度）和抽样方法（如Metropolis）

_ = pm.autocorrplot(trace[:2000], varnames=['mu'])

看完本文有收获？请转发分享给更多人

关注「Python开发者」，提升Python技能