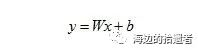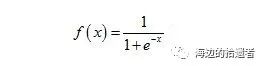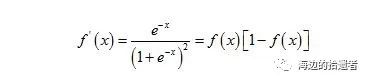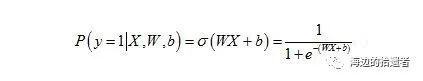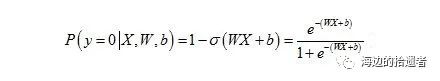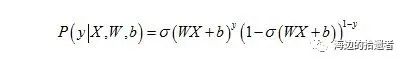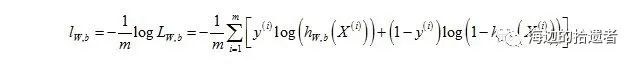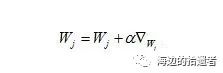逻辑回归算法原理及实现

2020 年 5 月 2 日 图与推荐

点击上方“海边的拾遗者”，选择“星标”公众号

第一时间获取价值内容

在典型的分类算法中，一般为监督学习，其训练样本中包含样本的特征和标签信息。在二分类中，标签为离散值，如{-1,+1}，分别表示负类和正类。分类算法通过对训练样本的学习，得到从样本特征到样本标签之间的映射关系，这也被称为假设函数，可利用该函数对新样本进行预测类别。

Logistic Regression

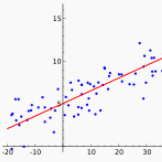
对于一个分类问题，通常有两种情况，线性可分和线性不可分。Logistic Regression模型属于广义线性模型的一种，一般线性可分的情况都能找到一个表示线性的超平面函数。以特征只有一维的数据为例，其线性可分的超平面形式为：

其中W为权重，b为偏置。若在多维的情况下，两者均应表示为向量的形式。在该算法中，通过对训练样本的学习，最终得到该超平面，将数据分为两个不同的类别。在这里，可引入阈值函数来将样本映射到不同的类别中，最常见的函数以Sigmoid函数为例，形式如下：

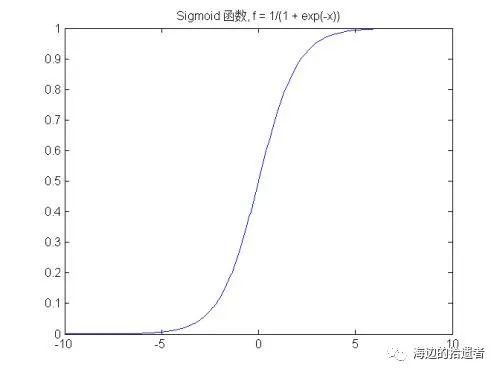
该函数可视化之后如下：

从图像中可以看到，该函数的值域为(0,1)，在0附近的变化比较明显。其导函数则为：

现在让我们用代码实现该函数：

import numpy as npdef sigmoid(x):    return 1.0 / (1 + np.exp(-x))

对输入向量X来说，其属于正类的概率为：

其中ɕ代表Sigmoid函数，则输入向量X属于负类的概率为：

损失函数

对Logistic Regression来说，可以通过观察上面输入向量X所属类别概率可得到概率表达函数：

其中W和b在上面的函数形式中是比较难求解的，需要先将其用极大似然法进行估计，将之转化成凸函数(此处是凸优化中的理论)，即W和b存在最优解，也便于用较简单的方法求解。对其似然函数取负的Log后函数形式为：

其中h为输入向量传入Sigmoid函数后的值，所以我们只需要求使得l_w,b最小时的W和b。

梯度下降法

对损失函数求最小值的问题，可选用迭代法中的梯度下降法来求解，其优点在于只需求解损失函数的一阶导，计算成本相对牛顿法之类的要小，这使得其能在大规模数据集上得到广泛应用。具体原理为根据初始点在每一次迭代的过程中选择下降的方向，进而改变需要修改的参数。

两个变量的梯度表达式为：

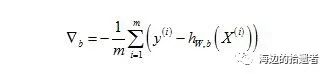
其中b可以当做W中的第一个分量，其更新公式为：

现在可以用代码实现训练的具体过程：

def lr_gd(feature, label, maxCycle, alpha):    '''input:  feature特征            label标签            maxCycle最大迭代次数            alpha学习率     output: w权重'''    n = np.shape(feature)[1]    w = np.mat(np.ones((n, 1)))    i = 0    while i <= maxCycle:        i += 1        h = sigmoid(feature * w)        err = label - h        if i % 100 == 0:            print("\t---------iter=" + str(i) + \            " , train error rate= " + str(error(h, label)))        w = w + alpha * feature.T * err    return w

其中误差函数为error，因为每次迭代均需计算当前模型的误差，具体实现如下：

def error(h, label):    '''input:  h预测值            label实际值    output: err/m错误率'''    m = np.shape(h)[0]       sum_err = 0.0    for i in range(m):        if h[i, 0] > 0 and (1 - h[i, 0]) > 0:            sum_err -= (label[i,0] * np.log(h[i,0]) + \                        (1-label[i,0]) * np.log(1-h[i,0]))        else:            sum_err -= 0    return sum_err / m