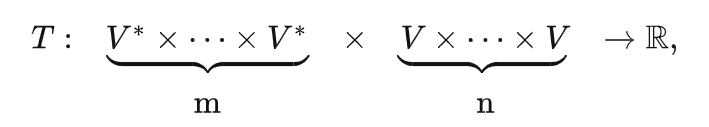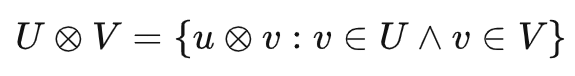卷到纯数学：大佬亲历总结的AI工程师纯数学课程学习之路

2022 年 11 月 22 日 新智元

新智元报道

作者：Frank Ding

编辑：QQ

【新智元导读】纯数学最容易懂的大学公开课和教程学习路线。

在入门机器人视觉和机器人运动后，开始逐步接触到了3D计算机视觉中的高阶数学概念，包括三维物体到二维图片的变换（术语称之为射影几何）；三维欧氏空间的物体运动坐标系变换，分为主动变换（active）和被动变换（passive）；另外在更高阶的计算机渲染中常会用到Mesh和黎曼曲面；此外，几何深度学习（Geometric Deep Learning）中也涉及到群论，李群等。这些迷之概念使得我对于本科高等数学课程（多元微积分，线性代数，概率论）后面的纯数学感到兴趣。本来一直觉得纯数学会非常难学，但是当我写了很多年代码和阅读了多个AI领域的众多论文之后，总有一些本质问题萦绕在心，得不到解释：

代码抽象的极限在哪里？高阶纯函数编程？
深度学习多个领域（CV，NLP，RL，GNN）是否有统一视角？目前深度学习的论文汗牛充栋，既有很多相似的pattern，也有每个领域的特性，是否有通用设计原则

第一个问题在范畴论（category theory）中广泛探讨，不过范畴论过于深奥，是抽象代数后的一门纯函数编程的理论基础。第二个问题在几何深度学习中被探讨。不过，这两个问题肯定不会被完全回答。即使无法得到最好的解释和回答，对于这些根本问题的探究的阶段性成功也是非常有意义的。正如理查德·费曼的名言：

I would rather have questions that can't be answered than answers that can't be questioned

为了让AI从业人员乃至程序员能进阶掌握高阶数学的武器，我斗胆总结一份从我这个非数学系的理工毕业生角度出发的自学纯数学指南。以下所有课程视频都已经搬运到了我的B站频道MyEncyclopedia公号中，此外，视频课程有对应教材的也一并列出。

在学习这些知识时候，发现之间的联系是非常广泛的，这个倒是非常出乎我意料，也让学习非常有成就感。以下总结了若干贯穿所有领域的重要概念。

群的最一般概念和离散数学群
群论体系下构建的抽象代数结构
有限维向量空间的线性映射和基变换，并且此视角下的矩阵（线性代数）理解
从基变换的角度理解傅里叶变换，即傅里叶变换是函数表示的特殊的基。
有限维向量空间上定义了距离（内积空间）后，向量空间有了几何结构。
从线性映射推广到多变量线性映射（multilinear map），这是张量（Tensor）的数学意义
从离散数学群论到连续函数映射，形成了微分流形（Differential Manifold）的概念。在此基础上进而发展出了李群，本质是为了解决例如旋转矩阵群虽然在乘法上封闭（因此组成群）但是在加法上不封闭的问题。
一般群论扩展出范畴论，这是函数式编程的数学原理。

学习顺序

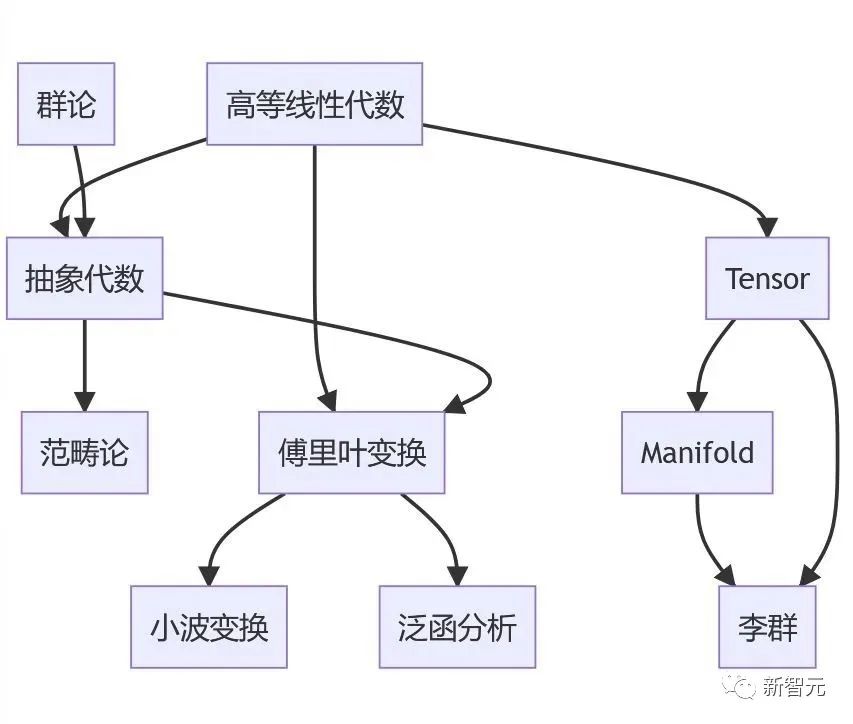
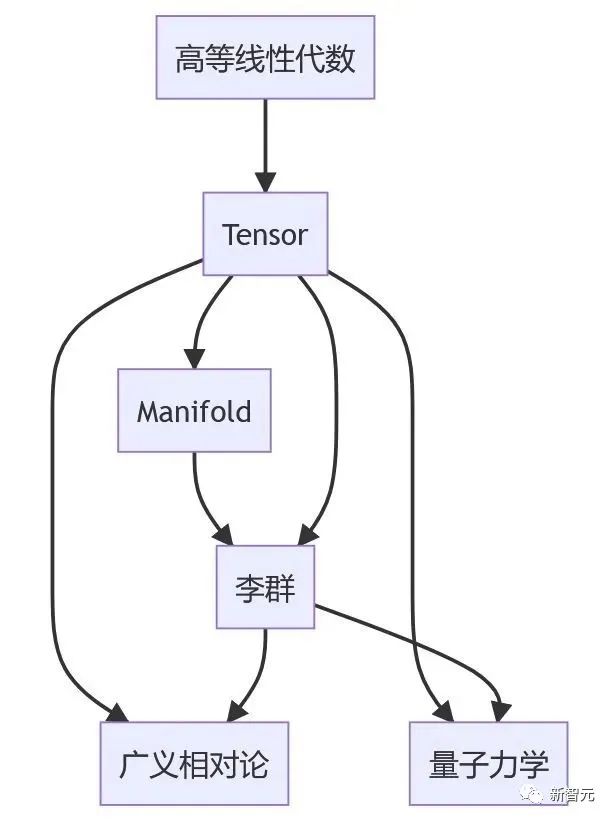
下图为我推荐的课程学习顺序。

当对张量和李群掌握充分后，原则上可以更上一层楼，学习广义相对论和量子力学。不过我并没有计划涉足这两个艰深的领域，也就不多言了。

线性映射下的高等线性代数

【Sheldon Axler】线性代数应该这样学

B站链接

https://www.bilibili.com/video/BV1Dm4y1c7Cn

评价

本课程的教师是配套同名教材线性代数应该这样学（Linear Algebra Done Right）这本书的作者。课程和教材都是从线性映射(linear map)角度来看待矩阵。由最基本的向量空间和内积空间定义出发导出对偶空间（Dual Space），特征值，特征根，对角矩阵，正交基，直到最核心的谱论（Spectral theorem）。此课程说实话不适宜第一次学线性代数的同学。同时，不适合数学系的，因为跟高代相比太浅；不适合工程类的，因为太深而且没有跟应用联系起来。但是，本书却广受赞誉，中文也有翻译本。其最大的特点是通过空间变换和矩阵联系起来，从最基本的定义导出矩阵中的最核心概念：特征值，特征根，对角矩阵，正交基等。

配套教材

【Nathaniel Johnston】 Advanced Linear Algebra

B站链接

https://www.bilibili.com/video/BV1uV4y157XE

评价

课程关于线性映射背后的基变换等讲述的非常清楚。不过对比Nathaniel Johnston的教材Advanced Linear Algebra and Matrix Algebra来说，视频课程只涉及到教材的一二章的内容，但并没有涉及到第三章Tensor的部分，有点可惜。视频包含很多向量空间和线性映射的例子和证明，可以作为线性代数应该这样学的很好补充。同时推荐教材第三章Tensor，适合作为Tensor概念的入门理论学习。

配套教材

【Matthew Macauley】Advanced Linear Algebra

B站链接

https://www.bilibili.com/video/BV1Me4y1a7Uk

评价

Matthew Macauley教授讲课节奏条理都很赞，示例也比较充足，他的多个数学课程都很棒，尤其是下面群论部分的Visual Group Theory最为经典。本课程可以作为上述两门自成体系的课程很好的补充，尤其是Tensor作为multilinear map的部分。课程对应教材为Peter Lax的经典老教材线性代数及其应用。

配套教材

群论，抽象代数

【Matthew Macauley】可视化群论

B站链接

https://www.bilibili.com/video/BV1ka411378X

配套教材

评价

课程基于Nathan Carter负有盛名的Visual Group Theory 这本非常非常棒的群论入门书。视频课程本身在教材的基础上补充了不少例子和定理证明，使抽象难以理解的群里严重降低了入门难度。我作为同时仔细看过视频和教材的读者，觉得视频课程有以下几个优势：首先是建立概念时一步一步带你walk through，比如最核心的群同态概念，使得概念的建立更加深刻形象；其次课程补充了不少代数方法的严格证明，有的时候，代数方法比视觉方法更显示了问题的本质和联系。强烈推荐视频和教材，因为群论是现代数学的基石。

【哈佛Benedict Gross】抽象代数

B站链接

https://www.bilibili.com/video/BV1Yt4y1F72S

评价

很老的课程了，对应的教材为经典的 Michael Artin 的代数。学完本视频和配套教材会对抽象代数有扎实深入的理解。

配套教材

张量

张量是广义相对论的描述工具之一，另一个是黎曼几何。张量有其物理意义和数学意义，这里我们关注其数学意义而非物理意义。

张量是多重线性映射，其中，V是矢量空间，V*是对偶空间。

有了多重空间的线性映射，下一步就是将两个张量组成新的空间，这个空间由张量积得到

注意，张量积后的新空间的维度为原来两个空间的维度乘积，即若上述 U, V 分别是 m 和 n 维线性空间，则新空间维度为 mn。

eigenchris 系列

B站链接

【eigenchris】 Tensors for Beginners
https://www.bilibili.com/video/BV1zW4y1n7Cy
【eigenchris】 Tensor Calculus
https://www.bilibili.com/video/BV1Ae4y167ty

评价

eigenchris 的 tensor 入门系列讲的应该是最好理解的，举了很多具体的例子，例如关于重要的概念行向量作为covector。

XylyXylyX

B站链接

【XylyXylyX】 What is a Tensor
https://www.bilibili.com/video/BV1NK411Q7p4

XylyXylyX

B站链接

【XylyXylyX】 Lie Groups and Lie Algebras
https://www.bilibili.com/video/BV1Z14y1j78c

评价

XylyXylyX的李群视频是众多李群入门中比较不错的，有不少重复，适合初学。配套 Robert Gilmore的如下教材（教材后面部分过于复杂）。

配套教材

Jonathan Evans

B站链接

https://www.bilibili.com/video/BV1FK411D7dv

配套教材

视频有专门一节推荐了众多不错的教材，不过李群这个领域过于深奥，我也只是刚入门。因此在此仅列其一：Springer 的GTM（研究生数学系列）表示理论

傅里叶变换

傅里叶变换的本质是将函数分解成一组相对卷积算子的对角化基，是进阶泛函分析的重要概念。

【斯坦福 Brad Osgood】傅里叶变换和应用

B站链接

https://www.bilibili.com/video/BV1Gm4y1A7bw

配套教材

可由下方地址下载

https://see.stanford.edu/materials/lsoftaee261/book-fall-07.pdf

微分流形

XylyXylyX

B站链接

https://www.bilibili.com/video/BV1fG411E7Tc

程序员的范畴论

B站链接

【Bartosz Milewski】 Category Theory for Programmers
https://www.bilibili.com/video/BV1v14y1e7et
【Bartosz Milewski】 Category Theory for Programmers II
https://www.bilibili.com/video/BV14P4y1Z7Ci
【Bartosz Milewski】 Category Theory for Programmers III
https://www.bilibili.com/video/BV1gB4y1n72g