【论文笔记】基于BERT的知识图谱补全

作者：Yanfei Han

请关注专知公众号（点击上方蓝色专知关注）

• 后台回复“KGBERT” 就可以获取本篇论文下载链接~ 

论文动机

基于知识图谱的不完整性，这篇论文提出了一种使用预先训练好的语言模型用于知识图谱的补全的方法。即将知识图谱中的三元组视为文本序列，提出了一种基于Transformer知识图谱双向编码器表示(KG-BERT)的框架，通过这种新的框架对三元组进行建模。这种方法采用将一个三元组中的实体和关系描述作为输入，通过使用KG-BERT语言模型计算该三元组的得分函数。在多个基准知识图谱上的实验结果表明，该方法在三元组分类、链接预测和关系预测任务中均能取得了迄今为止最好的结果。

模型

为了充分利用上下文表示丰富的语言模式以及在知识图谱补全任务取得更好的效果，我们微调预先训练的BERT。我们将实体和关系表示为它们的名称或描述，然后用名称或者描述的词序列作为微调的BERT模型的输入语句。为了对一个三元组的合理性进行建模，我们把(h,r,t)作为一个单独的序列。序列是指对BERT的输入标记序列，它可以是两个实体名称/描述的语句，也可以是(h,r,t)组合在一起的三个语句。

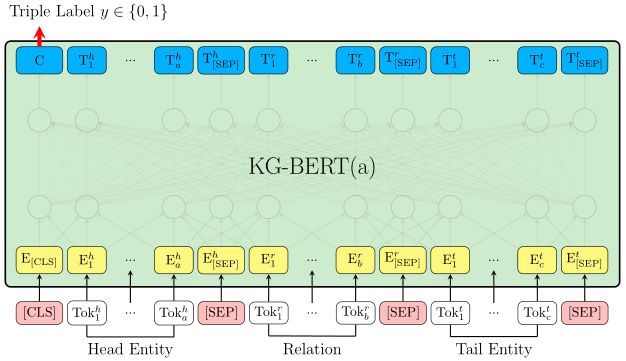
图1 基于微调KG-BERT预测一个三元组合理性的简要说明

用于对三元组建模的KG-BERT结构是如图1所示。我们将这个KG- BERT版本命名为KG- BERT(a)。对于给定的标记，通过对相应的标记、分割和位置嵌入求和来构造其输入表示。由[SEP]分隔的不同元素具有不同的分割嵌入。头尾实体句中的标记共享同一分割嵌入e_A，但是对于关系语句的标记拥有不同的分割嵌入e_B。对于同一位置i的不同标记拥有相同的位置嵌入。每一个输入标记i都有一个输入表示E_i。然后将这些标记表示全部输进BERT模型结构。特殊[CLS]标记和第i个输入标记的最终的隐藏向量分别表示为C属于R_H和T_i属于R_H，其中H为预训练BERT中的隐藏状态的大小。采用[CLS]对应的最终隐藏状态C作为计算三元组分数的聚合序列表示。在三元组分类微调唯一引入的新参数是分类层权重W属于R_2xH。对于一个三元组的得分函数t=(hr,t)是s_t=f(h,r,t)=sigmoid(CW_T)，其中，s_t属于R_2，是一个2维的实向量且s_t0，s_t1属于[0,1]，s_t0 + s_t1=1。对于给定的正三元组集合D_+和构建相对应的负三元组集合D_-，我们可以计算带有s_t和三元组标签的交叉熵损失：

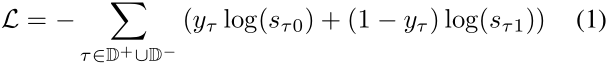
其中，y_t属于{0,1}是三元组的标签（正例或者负例）。负三元组集合D_-是通过将正三元组集合中的头实体或者尾实体随机替换为其他的实体h_'或者t_'生成的，即：

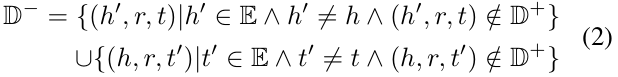
其中E是实体的集合。如果一个三元组不在正三元组集合中将视为负例。对于预训练的参数权重以及新权重都是通过梯度下降更新的。

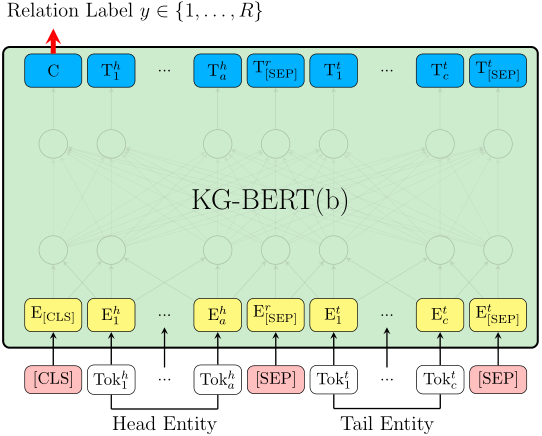
图2 基于微调KG-BERT预测两个实体之间关系的简要说明

用于预测关系的KG-BERT的体系结构如图2所示。我们将这个KG- BERT版本命名为KG-BERT(b)。我们只用两个实体h和t的句子来预测它们之间的关系r。在我们的初步实验中，我们发现直接预测与两个实体的关系要优于使用关系损坏的KG-BERT(a)，即通过将关系r随机替换为r_'生成负三元组。对于KG-BERT(a)，会将与[CLS]对应的最终隐藏状态C作为两个实体的表示。在关系预测的微调中唯一引入的新参数是分类层权重W_'属于R_RxH，其中R是在一个KG中关系的的数目。对于一个给定三元组t=(h,r,t)得分函数是s_t'=f(h,r,t)=softmax(CW_T')，s_t'属于R_R是一个R维的实向量且s_ti'属于[0,1]和s_t1'+s_t2'+...s_tR'=1。我们可以计算带有s_ti’和三元组标签的交叉熵损失：

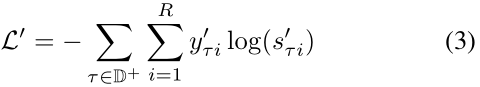
其中t是属于正三元组的，y_ti'是三元组t的指示器，当r=i时，y_ti'=1和当r!=i时，y_ti'=0。

实验

为了验证KG-BERT模型的效果，这篇论文的实验主要是从三元组分类，链接预测，关系预测三方面展开，使用的数据集如表1所示。使用平均排名（MR）和Hits@n作为评价标准。三元组分类，链接预测，关系预测具体实验体结果如下所示：

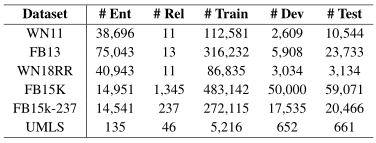
表1 数据集的汇总统计

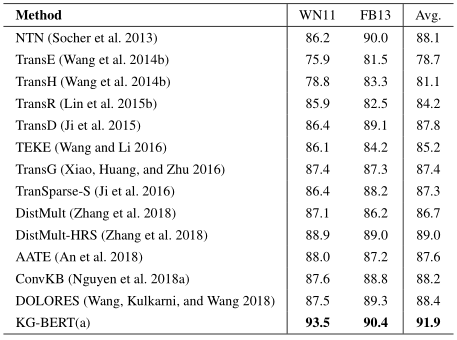
表2 不同嵌入方法的三元组分类精度(以百分比为单位)。基线结果是从相应的论文中获得。

KG-BERT(a)表现良好的主要原因有四个方面:1)输入序列同时包含实体和关系词序列；2)三元组分类任务与BERT 预训练中的下一个句子预测任务非常相似，在大的自由文本中捕捉两个句子之间的关系，因此预训练的BERT权值很好地用于推断三元组中不同元素之间的关系；3)标记隐藏向量是上下文嵌入。同一标记在不同的三元组中可以有不同的隐藏向量，因此上下文信息能够准确使用。4)自注意机制可以挖掘出与三元组事实相关的最重要的词。

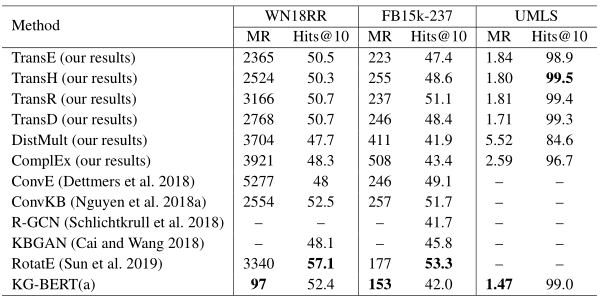
表3  在WN18RR、FB15k-237和UMLS数据集上链接预测的结果。基线模型的结果(我们的结果)是使用OpenKE工具包实现的，其他基线结果来自原论文

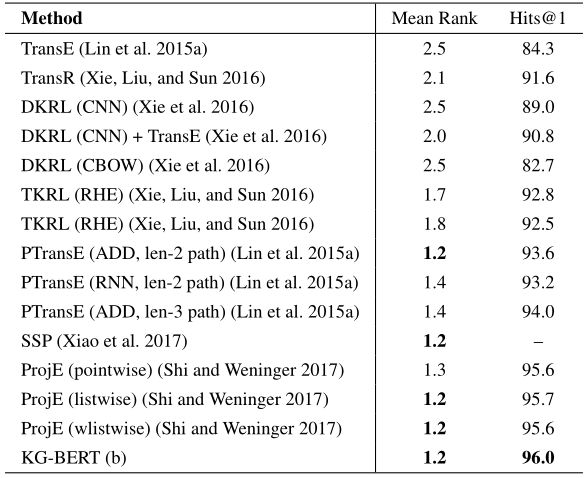
表4 在FB15K数据集上的关系预测结果。其他基准结果来自原论文。

讨论

从实验结果可以看出，KG-BERT在KG的三种补全任务中都能取得较好的性能。然而，BERT模型的一个主要的限制是其链接预测评估耗时较长，因为几乎需要替换所有的头实体或尾实体，并且所有损坏的三元组序列都要被送入Transformer模型的第12层。可能的解决方案是引入1-N个评分模型，如ConvE或使用轻量级语言模型。

总结

这篇论文提出了一种新的知识图谱补全方法——知识图谱BERT (KG-BERT)。将实体和关系表示为它们的名称/描述文本的序列，并把知识图谱补全问题转化为序列分类问题。KG-BERT可以在大量的自由文本中利用丰富的语言信息，并且能够突出连接三元组的最重要的单词。该方法通过在多个基准KG数据集上超过最先进的结果证明其具有良好的应用前景。

论文链接：

https://arxiv.org/abs/1909.03193

-END-

专 · 知

专知，专业可信的人工智能知识分发，让认知协作更快更好！欢迎登录www.zhuanzhi.ai，注册登录专知，获取更多AI知识资料！

欢迎微信扫一扫加入专知人工智能知识星球群，获取最新AI专业干货知识教程视频资料和与专家交流咨询！

请加专知小助手微信（扫一扫如下二维码添加），加入专知人工智能主题群，咨询技术商务合作~

专知《深度学习:算法到实战》课程全部完成！560+位同学在学习，现在报名，限时优惠！网易云课堂人工智能畅销榜首位！

点击“阅读原文”，了解报名专知《深度学习:算法到实战》课程