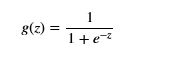LR背后的原理浅析

会员服务 ·

LR背后的原理浅析

2017 年 10 月 24 日 Python技术博文 Anne

现实生活中经常遇到最优化问题，如怎么用最短的时间从A地到达B地；如何投入最少工作却获得最大受益；如何设计发动机使得耗油量最少二功率最大等，可见最优化作用十分强大。

”回归“一词源于最佳拟合，表示要找到最佳拟合参数集。训练分类器时的做法就是寻找最佳拟合参数，使用的是最优化算法。

logistic回归的一般过程

1：收集数据

2：准备数据：由于需要进行计算距离，因此要求数据类型为数值型。

3：分析数据

4：训练数据：大部分时间用于训练，训练的目的是为了找到最佳的分类回归系数。

5：测试算法

6：使用算法：首先，我们需要输入一些数据，并将其转换成对应的结构化数值；接着，基于训练好的回归系数就可以对这些数值进行简单的回归计算，判定他们数据哪个类别；在这之后，就可以在输出的类别上做一些其他的分析工作。

logistic回归

优点：计算代价不高，易于理解和实现。

缺点：容易欠拟合，分类精度可能不高。

使用数据类型：数值型和标称型数据。

Sigmoid函数由来

在二分类的情况下，分类函数会输出0或者1（0代表一个类别标签，1代表另一类的类别标签）。这类分类函数你可以想到单位阶跃函数（Heaviside step function）。而该函数问题在于他是从0直接瞬间跳到1的，函数不可导。而Sigmoid函数：

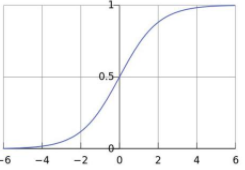
图像：

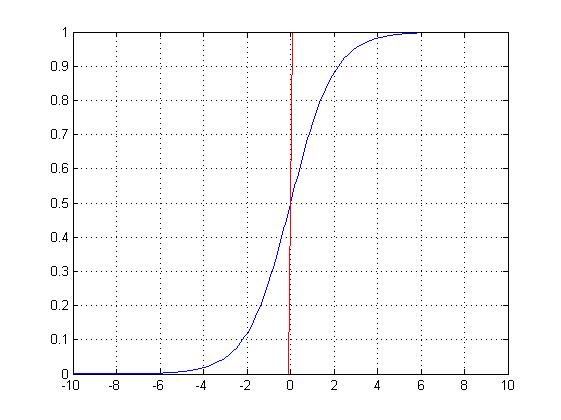
它随着z的增大，对应的Sigmoid值将逼近于1；而随着z的减小而逼近于0；看起来想阶跃函数；

为了实现Logistic回归分类器，可以在每个特征上都乘以一个回归系数，然后把所有的结果值相加，将这个总和代入Sigmoid函数中，进而得到一个范围在0~1之间的数值。任何大于0.5的数据被分为1类，小于0.5即被归入0类。所以，逻辑回归也可以被看作是一种概率估计。

最优化算法 梯度下降的直观解释

Gradient Descent

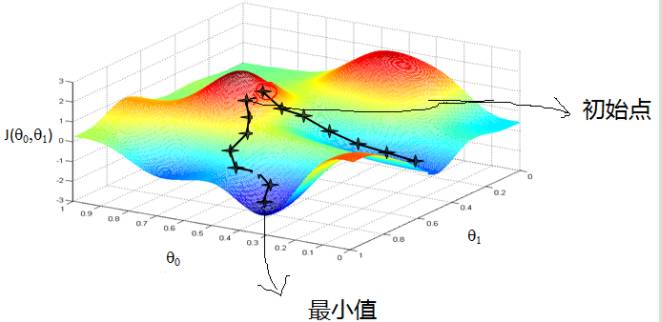
比如我们在一座大山上的某处位置，由于我们不知道怎么下山，于是决定走一步算一步，也就是在每走到一个位置的时候，求解当前位置的梯度，沿着梯度的负方向，也就是当前最陡峭的位置向下走一步，然后继续求解当前位置梯度，向这一步所在位置沿着最陡峭最易下山的位置走一步。这样一步步的走下去，一直走到觉得我们已经到了山脚。当然这样走下去，有可能我们不能走到山脚，而是到了某一个局部的山峰低处。

从上面的解释可以看出，梯度下降不一定能够找到全局的最优解，有可能是一个局部最优解。当然，如果损失函数是凸函数，梯度下降法得到的解就一定是全局最优解。