计算一列数字的平均值

考虑一下下面的的问题：

你有一列浮点类型的数字。这绝不是令人讨厌的恶作剧----没有无穷个数字或无限大的数字，仅仅只是正常的“简单的”浮点型的数字。
现在：计算其平均值。你能做到吗？

事实证明这是一个很困难的问题，想要得到该平

使用Hypothesis库来考虑以下的测试案列：

这并不是关于正确性的测试，只是测试平均值是否在列表的合理的限制范围内：在不作为平均值的情况下，有许多函数可以满足这个要求。最小值和最大值函数都满足这个要求，中值函数也是如此。

然而，几乎没有人的平均值计算方法满足这个要求。

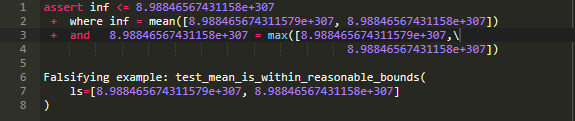
为了理解其中的原因，写下了我们自己的平均值计算方法：

这看起来十分合理--它正是平均值的定义--但是，它是错误的：

其问题在于有限的浮点数可能足够大，以至于它们的和溢出到无穷大。然后当你用无穷大除以一个有限的数时，你仍然会得到无穷大，这就意味着超出了范围。

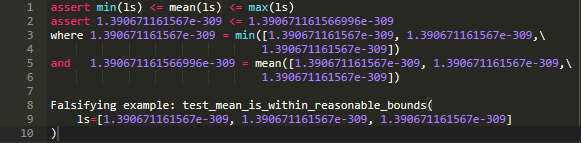
所以，为了阻止有限的浮点数之和的溢出，我们尝试通过列表的长度来限制我们的数字大小：

在这种情况下，你遇到的问题不是溢出，而是浮点数的精度不够：浮点数只能精确到一个整数的2次幂，因此除以3会导致舍入错误。在这种情况下我们有一个问题，就是（x/3）* 3一般不等于x本身。

所以，现在我们理解了为什么求平均值可能非常困难。让我们看看现有的方法是如何满足这个测试的。

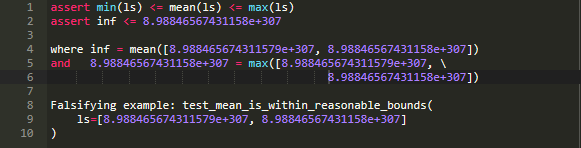
首先，我们尝试使用numpy库：

这遇到了我们在第一次实验中遇到的问题：

Python3.4还提供了新的统计模块。糟糕的是，这个模块也出现了问题（在Python3.5.2中得到了修复）：

在之前溢出到无穷大的情况下，这反而会产生一个错误。该错误产生的原因是统计模块在内部将所有数字都转化成Fraction类型，这是一种任意精度的有理数类型。由于一些细节，即在何时何地被转化为浮点数，这就产生了一个不容易被转化为浮点数的有理数。

编写一个通过测试的方法相对容易，仅仅需要简单的作弊，而不需要实际计算出其平均值：

也就是说，将值限制在期望的范围内。

然而，编写一个真正地，正确的平均值计算方法（可以通过测试的）是相当困难的：

为了理解其困难程度，这里有一篇30页的关于计算两个数的平均值的论文。

如果我是你，我就不会去看那篇论文。我已经阅读过这篇论文了，但我并没有记得很多细节。

这个测试是一个很好的实例：一旦你编写的代码没有崩溃，测试工作正常进行，就可以开始在结果值上添加额外的约束。正如本例所示，即使你添加的约束非常宽松，它也常常会捕获到一些有趣的bug。

它还证明了一个问题：浮点数运算非常困难，这使得它不太适合用Hypothesis库进行验证。

这并不是因为Hypothesis库不擅长测试浮点代码，而是因为它善于向人们展示编程的实际难度，而浮点编码比人们所预想的要难得多。

因此，你或许并不会在意它将发现的一些bug：一般来说，大多数人对于浮点数错误的态度是，”那些数字好奇怪，我们并不真的在意它们。或许已经足够好了“。如果你希望你的浮点代码是正确的，那么数值敏感度分析工作是必不可少的，但是很少有人能够完成这种高要求的工作。

我过去经常用这个例子来向人们演示Hypothesis库，但由于这些问题，我不会再这样做了：告诉人们他们并不想要修复的bug，既不会修复bug，也不会得到朋友。

但是，值得知道的是，这是一个问题：编程是非常困难的，而忽略这些问题并不会使它变得容易。你可以忽略正确性问题，直到它们真正给你造成麻烦为止，但是当它们给你带来麻烦时，最好不要感到惊讶。

而且，一些通用的技术也值得被牢记，因为这不仅仅是对浮点数有用：大多数的代码可以从中受益，而且大多数时候它告诉你的bug不会那么令人不快。

英文原文：https://hypothesis.works/articles/calculating-the-mean/  

译者：Lyx