REALM后续：最近邻搜索，MIPS，LSH和ALSH

2020 年 2 月 23 日 AINLP

上一篇介绍REALM的文章有几个遗憾。一个是今年ICML审稿并没有结束，所以标题不太好；二是对文中提到的Maximum Inner Product Search没有作充分的介绍。发出去的标题已经没法改了，这篇文章介绍一下MIPS和最近邻搜索问题，以及两个相关的算法。

提示：长公式可以左右滑动查看哦

问题定义

MIPS的定义很简单，假设你有一堆d维向量，组成集合X，现在输入了一个同样维度的查询向量q (query)，请从X中找出一个p，使得p和q的点积在集合X是最大的。用公式写出来就是

p=\mathop{\arg\max}_{x \in X}x^Tq

p=\mathop{\arg\max}_{x \in X}x^Tq

p=\mathop{\arg\max}_{x \in X}x^Tq

p = \mathop{\arg\min}_{x \in X}\left \|q-x\right\|^2=(\left \| x \right \|^2 - 2q^Tx)

p = \mathop{\arg\min}_{x \in X}\left \|q-x\right\|^2=(\left \| x \right \|^2 - 2q^Tx)

朴素的算法

对于MIPS问题，一个直观的蛮力算法就是计算出所有相关的内积，然后将内积排序，找到最大的那个。对于最近邻问题其实也类似，即使X中向量模长各不相同，也可以提前计算出来，并不会增加排序的时间复杂度。

内积的计算可以转换成一个矩阵乘法，在CPU和GPU上都有大量的高效实现。当X中有N个向量时，时间复杂度是O(Nd)，当N不大的时候是可以接受的，但是通常在工业界的大规模系统中，X的规模往往很大，朴素算法就显得力不从心。

Locality-sensitive hashing

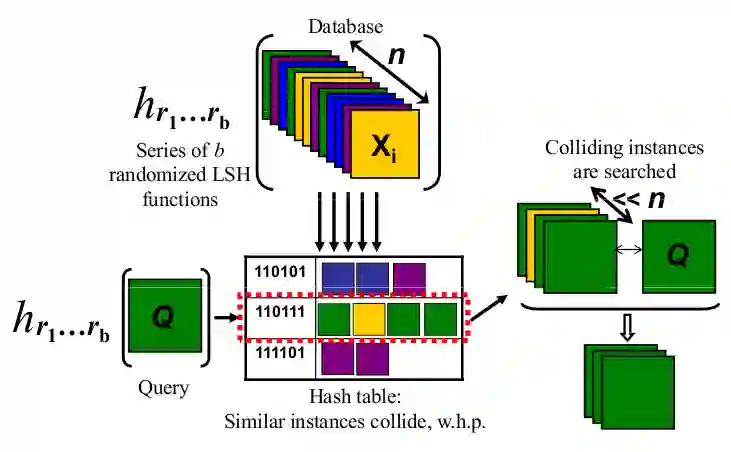
对于某些距离度量（例如欧式距离，cosine距离）下的最近邻问题，可以使用LSH算法来解决。LSH的思路就像下图示意的那样，用hash函数把高维空间的点分到几个桶里去，从而减少距离的计算量。

跟普通的哈希函数不同，这个哈希函数是Locality-sensitive的。具体地说就是它有一个神奇的特点：在空间中离得近的点被分到同一个桶的概率大，离得远的点则大概率被分到不同的桶里去。或者说对于两个点x和y，他们被哈希函数分到同一个桶的概率随着距离的增大单调递减。

这样在查询的时候，只需要精确地比较和查询向量q处在同一个桶里的那些x。如果桶足够多，那便可以将N大大降低，从而提高查询速度。但需要注意的是，LSH是一个近似算法，有可能产生桶内的向量其实都不是最优解的情况，不同哈希函数发生这种情况的概率都不一样，也是作为评价哈希函数好坏的重要依据之一，对这部分感兴趣的朋友可以读参考文献。

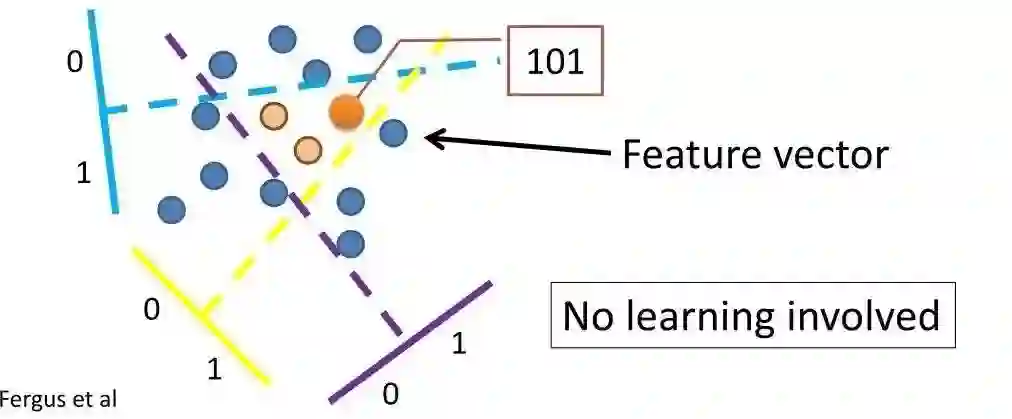
下面举一个具体的例子来解释一下LSH。假设某个最近邻问题考虑的距离度量是cosine距离，有一个满足要求的LSH函数（变换），称为Random Projection。

如上图所示，其过程很好理解：

随机取一个空间中的超平面将空间分为两半，X内位于某一半的点标为0，其他标为1；
重复第一步K次。

完成之后，X中的每个点便得到了一个由K个0，1组成的表示（signature）。例如重复了K=32次，那每个点都被分到了一个用一个int32类型的整数编号的桶里。如果这些点在空间中分布足够均匀，那么我们将可以期望每个桶里只有N/2^K个点，当K～logN，则查询的时间复杂度就约为O(dlogN)。

整个过程构建出了一张哈希表，由于LSH可能会错过最优解，一个可行的增强鲁棒性的做法是用同样的方法多构造几张哈希表，借助随机的力量来降低犯错的概率。参考阅读[3]是一个讲解LSH的视频，可谓短小精悍，直观易懂，推荐给大家。

LSH看上去相对于朴素算法确实前进了一大步。但别高兴得太早，要达到O(dlogN)的效果必须服从那个很强的假设。而点在空间中分布足够均匀往往是不太现实的。除此之外，一个LSH只能适用于某些距离度量，对于MIPS，找不到符合要求的LSH。

Asymmetric LSH(ALSH)

[2]里证明了找不到可用于MIPS问题的LSH函数，但他们发现对LSH稍作点改动即可将MIPS问题转变为欧式距离下的最近邻搜索问题。改动的关键就在于Asymmetric这个词。在LSH算法中，对查询向量q和X中的向量做的是同样（对称）的变换，而在ALSH中作者对两者使用了不同（非对称）的变换。

简单起见，假设查询向量q的模长是1。对于X，先做一个放缩变换使得X中所有向量x的所有元素都小于1。然后对X中的向量进行变换P(x)，对查询向量q做变换Q(x)，P和Q的定义如下：

Q(x) = [x;\frac{1}{2};\frac{1}{2},…,\frac{1}{2}]

Q(x) = [x;\frac{1}{2};\frac{1}{2},…,\frac{1}{2}]

Q(x) = [x;\frac{1}{2};\frac{1}{2},…,\frac{1}{2}]

上面就是ALSH的主要过程，它的核心技巧是通过“非对称变换”构造向量从而消除x向量模长对MIPS结果的影响。

前面为了简单起见引入了一个查询向量q必须是单位向量的约束，[2]中介绍了怎么进一步加强这个变换来消除这个约束，在此就不赘述了。

后记

LSH和ALSH的理论证明部分比较复杂，本文可能会有错误的地方。由于目前我们的粉丝数太少，还无法在文章留言，有什么意见和建议大家可以直接到公众号中给我们发消息。

除了本文介绍的LSH及其变种，在解决向量检索问题上还有很多有趣的算法和厉害的算法包，我们会在后续的文章中继续介绍。在今年一月份的时候Google发了一篇叫《Reformer: The Efficient Transformer》的文章，就用到了LSH的算法，近期我们可能也会乘热打铁介绍一下这篇文章。

参考阅读

国内向量检索引擎 Milvus

https://milvus.io/cn/docs/about_milvus/index_method.md
ALSH论文

https://papers.nips.cc/paper/5329-asymmetric-lsh-alsh-for-sublinear-time-maximum-inner-product-search-mips.pdf
LSH讲解视频（墙外）

https://www.youtube.com/watch?v=Arni-zkqMBA&list=PLZKSpah6NB5LbjWM9JoOSbZZffwCUwJdh&index=8
LSH ppt（Stanford）

https://graphics.stanford.edu/courses/cs468-06-fall/Slides/aneesh-michael.pdf
Reformer: The Efficient Transforme r

https://arxiv.org/pdf/2001.04451.pdf

推荐阅读

AINLP年度阅读收藏清单

【ICML 2020】REALM: Retrieval-Augmented Language Model PreTraining

大幅减少GPU显存占用：可逆残差网络(The Reversible Residual Network)

鼠年春节，用 GPT-2 自动写对联和对对联

用 GPT-2 自动写诗，从五言绝句开始

transformer-XL与XLNet笔记

AINLP-DBC GPU 云服务器租用平台建立，价格足够便宜

征稿启示 | 稿费+GPU算力+星球嘉宾一个都不少

关于AINLP

AINLP 是一个有趣有AI的自然语言处理社区，专注于 AI、NLP、机器学习、深度学习、推荐算法等相关技术的分享，主题包括文本摘要、智能问答、聊天机器人、机器翻译、自动生成、知识图谱、预训练模型、推荐系统、计算广告、招聘信息、求职经验分享等，欢迎关注！加技术交流群请添加AINLP君微信(id：AINLP2)，备注工作/研究方向+加群目的。