如何从数学角度理解知识图谱嵌入？中山大学等最新《知识图谱嵌入:表征空间视角》研究综述，32页pdf阐述代数、几何、分析下的KGE

知识图谱一直关注的研究热点。中山大学等最新《知识图谱嵌入:表征空间视角》研究综述，32页pdf阐述代数、几何、分析下角度的知识图谱嵌入，值得关注！

知识图谱嵌入(Knowledge graph embedding, KGE)是一种日益流行的技术，旨在将知识图谱中的实体和关系表示为低维的语义空间，在链接预测、知识推理和知识补全等领域有着广泛的应用。在本文中，我们对现有的基于表示空间的KGE技术进行了系统的回顾。特别地，我们基于表示空间的三个数学角度** (1)代数角度、(2)几何角度和(3)分析角度**建立了一个细粒度分类来对模型进行分类。在深入KGE模型及其数学性质之前，我们先介绍基本数学空间的严格定义。我们进一步讨论了这三类不同的KGE方法，并总结了空间优势如何在不同的嵌入需求中发挥作用。通过整理下游任务的实验结果，我们还探索了数学空间在不同场景下的优势及其背后的原因。进一步从表征空间的角度提出了一些有前景的研究方向，希望能启发研究者在设计KGE模型及其相关应用时更多地考虑其数学空间性质。

https://www.zhuanzhi.ai/paper/44427b32a1eea79e689822dd16ac0561

1. 概述

知识图谱是一种存储现实世界中事实知识的多关系图。KGs中的节点表示现实世界中的实体(如名称、事件和产品)，边表示实体之间的关系。通常，一个KG可以有效地存储为知识三元组，其中每个三元组由两个实体和它们之间的一个事实关系(即<头实体、关系、尾实体>)组成。例如,在三重< RNA病毒,子类,COVID-19 >, RNA病毒和COVID-19是现实世界的实体和子类RNA病毒和COVID-19代表之间的关系。近年来，大型KGs的建设出现了快速增长，如YAGO[94]、Wikidata[104]、Freebase[7]和DBepedia[2]。由于它们在存储和表示事实知识方面的有效性，它们已成功地应用于问答[91,132]、推荐系统[95,151]、信息检索[34,118]和其他特定领域的应用[58,68]。尽管KGs在表示结构化事实信息方面是有效的，但由于其大规模和复杂的图结构，它们很难操作。因此，如何有效、高效地从大规模KGs中提取和利用有用信息，用于下游任务，如链接预测[17,97,142]和实体分类[49,123,134]，是一项艰巨的任务。为了解决这一具有挑战性的任务，知识图谱嵌入(Knowledge Graph Embedding, KGE)技术被提出，并在机器学习领域受到了大量关注[10,17,48,62,73,97]。KGE的基本思想是学习将一个KG的实体和关系嵌入到一个低维空间中(即向量嵌入)，其中的嵌入要求保留原始KG的语义和关系结构。然后，可以利用学习到的实体和关系嵌入来解决下游应用，如KG补全[1,10,115,137,141]，问题回答[24,61,127,132,150]，信息提取[30,47,119,147]和实体分类[59,92]。

许多KGE技术被提出来学习KGs中实体和关系的嵌入[50,65,97,115,120]。一些KGE方法提出通过保留KGs中实体之间的关系模式来学习KG嵌入，例如，为了捕获实体之间的转换关系，提出了TransE[10]将KGs嵌入到欧氏空间中，并将实体之间的关系表示为向量空间中实体嵌入之间的平移向量。此外，为了保留和推断KGs中的其他关系模式，包括对称、反对称、反转和复合，RotatE[97]被提出将KGs映射到复向量空间中，其中关系表示为实体之间的旋转。

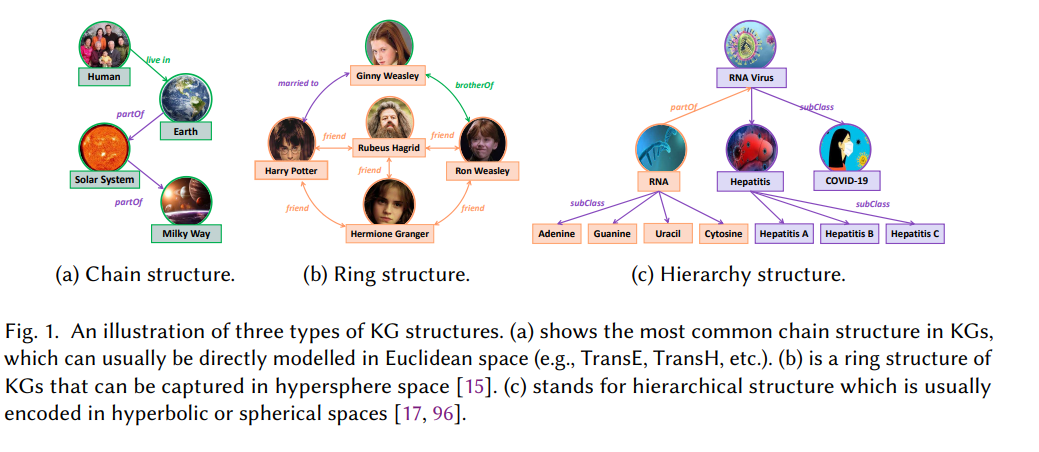
另一种KGE方法提出通过保留KGs的结构模式来学习KG嵌入，这一工作的动机是大型KGs通常包含许多复杂和复合结构。例如，在图1中，我们给出了KGs中三种典型的结构模式，即链结构、环结构和层次结构。为了有效地捕获知识图谱中的层次结构，提出了ATTH[3]将知识图谱嵌入到曲率可训练的双曲空间中，在双曲空间中可以使用比欧氏空间更丰富的变换来分离节点[76]，同时捕获逻辑模式。此外，一些KGE方法也尝试将KGs嵌入到其他数学空间中，以在KGs中建模一些理想的性质，如KG2E[45]是第一个“基于密度”的嵌入技术，它学习KGs在高斯分布概率空间中的嵌入，以建模实体和关系的不确定性。此外，TorusE[26]选择一个紧凑的李群作为其嵌入流形来处理正则化问题，ModulE[16]还引入了群理论，将实体和关系建模为群元素，这可以适应并优于大多数现有的KGE模型。从表示空间的角度，我们发现上述KGE方法大多学习在不同的数学空间(如欧氏空间、双曲空间和概率空间)中嵌入，以捕获KGs中不同的关系和结构模式，的确，不同的数学空间有其独特的优势，这有利于捕获KGs中不同的模式和属性，因此，我们认为表示空间在KGE方法中扮演着重要的角色。因为它决定了可以被KG嵌入捕获和保存的KG的模式和属性。除了KGE领域，一些研究[13,74,82]也证明了数学空间在传统机器学习中的重要性。

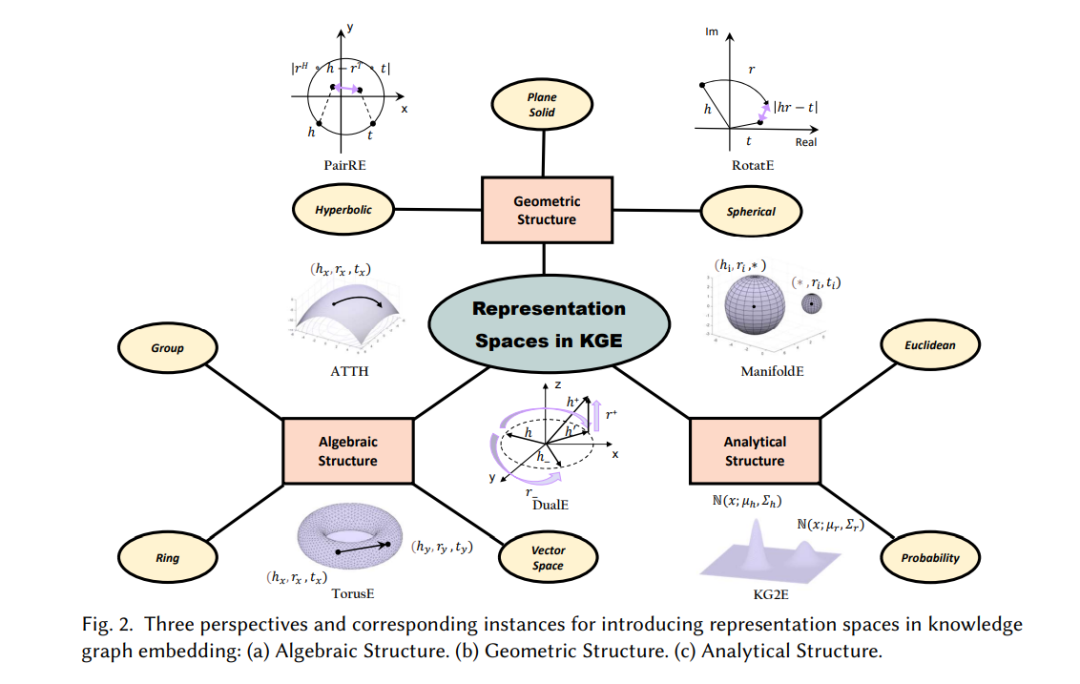
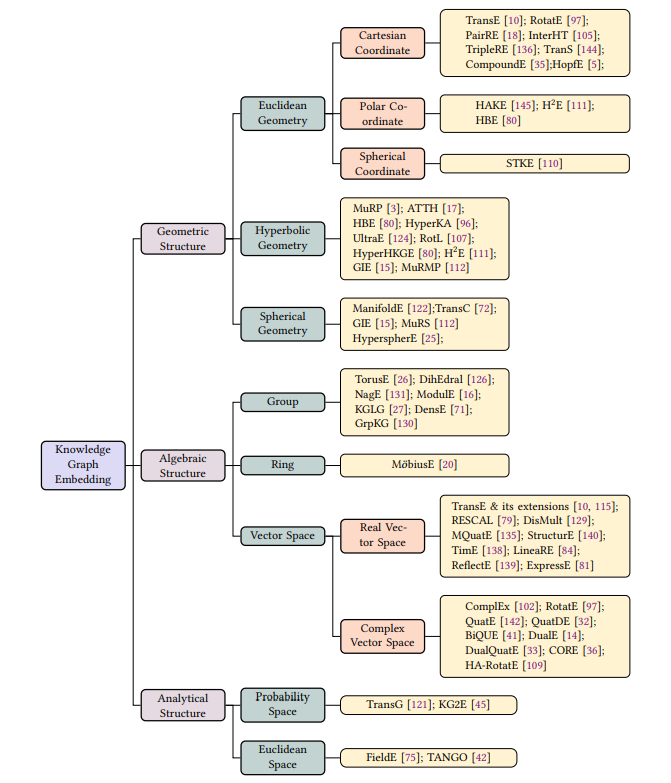
一些研究致力于从数学空间的角度讨论传统的机器学习模型[74,82]。然而，目前还没有从数学空间的角度对KGE方法进行系统的综述。现有关于KGE方法的研究主要集中在编码模型和KGE方法的应用上。例如Wang等[108]根据KGE方法的嵌入函数对其进行了分类，并将其分为三层:基于翻译的模型、语义匹配模型和附加信息模型。Ji等人[51]从表示学习、评分函数、编码模型和辅助信息四个方面全面介绍了KGE。Lu等人[70]调查了KGE方法，重点是利用文本信息。因此，本文旨在对知识图嵌入技术的表示空间进行全面综述，总结表示空间的不同性质，并为构建知识图嵌入方法提供指导。为了从新的空间视角更好地理解KGE方法，在基本数学空间系统的启发下，我们建立了一个系统的、全面的、多角度的分类法，根据现有KGE方法的表示空间对其进行分类。具体而言，我们建议将现有的KGE方法分为三类，即代数结构(algeaic Structure)、几何结构(Geometric Structure)和分析结构(Analytical Structure)。图2提供了我们的分类框架和属于每个类别的一些代表性KGE方法的概述(详细版本可以在第3节中找到)。在本综述中，我们将介绍上述三种数学结构的定义和性质，并详细介绍属于这些类别的一些代表性KGE方法。此外，我们将总结不同的KGE方法的实验结果，并为构建更有表现力和更强大的KGE方法提供一些建议和指导。此外，我们将从表示空间的角度指出KGE方法的新趋势和进一步的发展方向。

据我们所知，我们是第一个通过建立一个全面的数学空间结构来总结KGE模型的调研。综上所述，我们的工作贡献可归纳如下:

这是第一篇全面综述数学空间和KGE技术之间关系的论文。特别是，我们总结了KGE方法中不同数学空间的性质，以便清楚地了解它们在不同KGE方法中的数学性质。

我们根据现有的KGE模型的表示空间进行分类，同时从数学空间的角度对这些作品进行详细的描述和比较。

基于对不同空间本质属性的分析，我们为KGE任务提供了空间选择的思路，这可以帮助研究人员和实践者更好地理解空间特征，并为构建他们的KGE模型(包括损失函数、优化等)提供指导。

通过展示不同数学空间/结构中的一些独特性质，对KGE任务提出了一些建议和未来的发展方向。这些性质可以启发和推广到其他场景，如自然语言处理，transformer等，不仅是KGE任务。

本文的其余部分组织如下。第2节介绍了基本数学空间的符号和严格定义，以及它们之间的关系。本节将提供关于各种表示空间的一些初步知识，并在这些空间与KGE模型的三个关键组件(即嵌入映射、评分函数和表示训练)之间建立联系。由于基本数学空间无法覆盖现有KGE方法所使用的各种空间，我们从表示空间的角度开发了一个系统而全面的KGE方法分类框架。为了突出不同数学特征对KGE模型的出色作用，第3节介绍了提出的分类类别、不同空间的性质，并总结了空间优势在KGE模型中的作用。随后，第4节将介绍一些与空间相关的KG下游任务。通过结果，总结了数学空间在特定场景中的优势以及哪些特征对任务至关重要。最后，我们在第5节中提出了我们的结论和未来的工作，在其中我们总结了三种不同的数学结构各自的优点及其背后的原因，这将有助于启发我们在更多的领域构建最先进的算法，不限于KGE。

2. 知识图嵌入中的表示空间

由于KG通常包含许多复杂的结构(如1-to-N、N-to-N和层次关系)，研究人员提出将KG嵌入不同的表示空间，以更好地保存这些复杂的结构信息[17,26,41,122,142]。事实上，不同的表示空间有其独特的结构和属性，如我们在第2节中所示。但是，除了第2节中介绍的基本数学空间之外，还有更多的空间可以为KGE提供更好的属性。例如，在双曲空间中，区域和长度随半径呈指数增长，这为嵌入任务提供了更多的可用空间[3,17,76]。此外，在李群中，嵌入向量永远不会无限发散，因此有效学习[26]不再需要对嵌入向量进行正则化。因此，建立在不同表示空间上的KGE方法能够在原始KGs中捕获和保存不同的结构和归因信息。然而，从表示空间的角度对KG嵌入方法的系统综述还没有，也没有文献说明在特定KGE任务下如何正确选择表示空间。在本文中，我们旨在通过总结基于其数学表示空间的结构和性质的KGE方法来填补这一空白。

3. 知识图谱嵌入下游任务

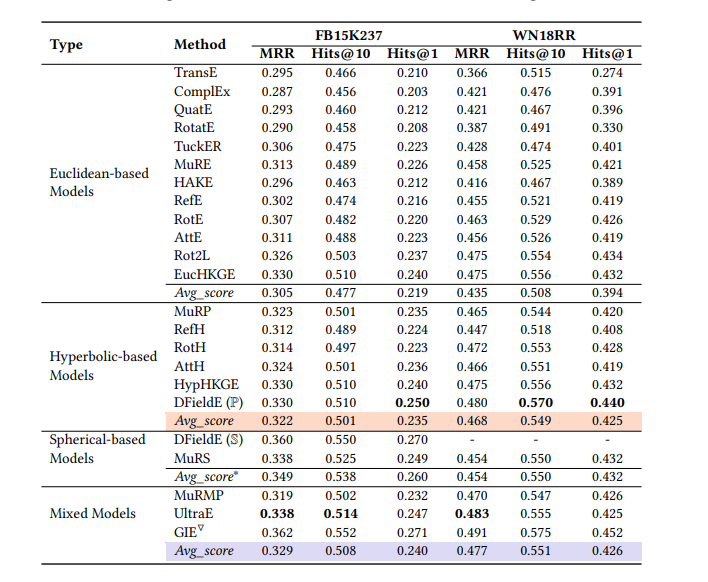
在从数学结构的角度对现有的KGE模型进行系统回顾之后，本节将重点介绍基于KGE的下游任务。我们强调了一些重要的和流行的应用，它们通常被用来评估嵌入模型的性能。在总结和比较了几种KGE模型的性能之后，从不同的空间角度分析了KGE模型的优缺点。在接下来的内容中，我们首先描述了链路预测的过程，这是KGE领域的一项基本任务，并重点介绍了一个流行的任务:链路预测场景中的层次获取。此外，我们还对模式推理的任务进行了分析和讨论。总结了数学特性在上述任务中的优势。