最新《图机器学习》综述论文，19页pdf

图是连接数据网络结构的一种常用表示形式。图数据可以在广泛的应用领域中找到，如社会系统、生态系统、生物网络、知识图谱和信息系统。随着人工智能技术的不断渗透发展，图学习(即对图进行机器学习)越来越受到研究者和实践者的关注。图学习对许多任务都非常有效，如分类，链接预测和匹配。图学习方法通常是利用机器学习算法提取图的相关特征。在这个综述中，我们提出了一个关于图学习最全面的概述。特别关注四类现有的图学习方法，包括图信号处理、矩阵分解、随机游走和深度学习。分别回顾了这些类别下的主要模型和算法。我们研究了诸如文本、图像、科学、知识图谱和组合优化等领域的图学习应用。此外，我们还讨论了该领域几个有前景的研究方向。

真实的智能系统通常依赖于机器学习算法处理各种类型的数据。尽管图数据无处不在，但由于其固有的复杂性，给机器学习带来了前所未有的挑战。与文本、音频和图像不同，图数据嵌入在一个不规则的领域，使得现有机器学习算法的一些基本操作不适用。许多图学习模型和算法已经被开发出来解决这些挑战。本文系统地综述了目前最先进的图学习方法及其潜在的应用。这篇论文有多种用途。首先，它作为不同领域(如社会计算、信息检索、计算机视觉、生物信息学、经济学和电子商务)的研究人员和从业者提供图学习的快速参考。其次，它提供了对该领域的开放研究领域的见解。第三，它的目的是激发新的研究思路和更多的兴趣在图学习。

图，又称网络，可以从现实世界中丰富的实体之间的各种关系中提取。一些常见的图表已经被广泛用于表达不同的关系，如社会网络、生物网络、专利网络、交通网络、引文网络和通信网络[1]-[3]。图通常由两个集合定义，即顶点集和边集。顶点表示图形中的实体，而边表示这些实体之间的关系。由于图学习在数据挖掘、知识发现等领域的广泛应用，引起了人们的广泛关注。由于图利用了顶点[4]，[5]之间的本质和相关关系，在捕获复杂关系方面，图学习方法变得越来越流行。例如，在微博网络中，通过检测信息级联，可以跟踪谣言的传播轨迹。在生物网络中，通过推测蛋白质的相互作用可以发现治疗疑难疾病的新方法。在交通网络中，通过分析不同时间戳[6]的共现现象，可以预测人类的移动模式。对这些网络的有效分析很大程度上取决于网络的表示方式。

一般来说，图学习是指对图进行机器学习。图学习方法将图的特征映射到嵌入空间中具有相同维数的特征向量。图学习模型或算法直接将图数据转换为图学习体系结构的输出，而不将图投影到低维空间。由于深度学习技术可以将图数据编码并表示为向量，所以大多数图学习方法都是基于或从深度学习技术推广而来的。图学习的输出向量在连续空间中。图学习的目标是提取图的期望特征。因此，图的表示可以很容易地用于下游任务，如节点分类和链接预测，而无需显式的嵌入过程。因此，图学习是一种更强大、更有意义的图分析技术。

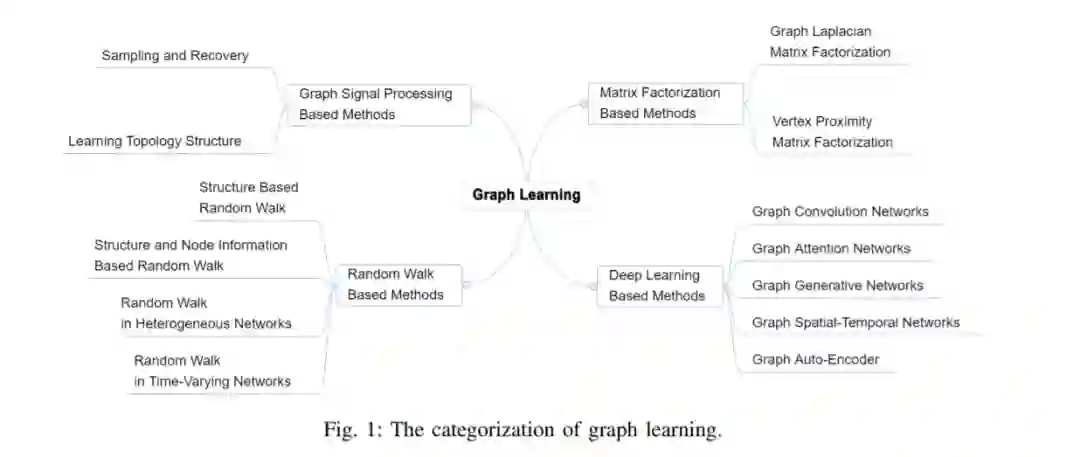
在这篇综述论文中，我们试图以全面的方式检验图机器学习方法。如图1所示，我们关注现有以下四类方法:基于图信号处理(GSP)的方法、基于矩阵分解的方法、基于随机游走的方法和基于深度学习的方法。大致来说，GSP处理图的采样和恢复，并从数据中学习拓扑结构。矩阵分解可分为图拉普拉斯矩阵分解和顶点接近矩阵分解。基于随机游动的方法包括基于结构的随机游动、基于结构和节点信息的随机游动、异构网络中的随机游动和时变网络中的随机游动。基于深度学习的方法包括图卷积网络、图注意力网络、图自编码器、图生成网络和图时空网络。基本上，这些方法/技术的模型架构是不同的。本文对目前最先进的图学习技术进行了广泛的回顾。

传统上，研究人员采用邻接矩阵来表示一个图，它只能捕捉相邻两个顶点之间的关系。然而，许多复杂和不规则的结构不能被这种简单的表示捕获。当我们分析大规模网络时，传统的方法在计算上是昂贵的，并且很难在现实应用中实现。因此，有效地表示这些网络是解决[4]的首要问题。近年来提出的网络表示学习(NRL)可以学习低维表示[7]-[9]的网络顶点潜在特征。当新的表示被学习后，可以使用以前的机器学习方法来分析图数据，并发现数据中隐藏的关系。

当复杂网络被嵌入到一个潜在的、低维的空间中时，结构信息和顶点属性可以被保留[4]。因此，网络的顶点可以用低维向量表示。在以往的机器学习方法中，这些向量可以看作是输入的特征。图学习方法为新的表示空间中的图分析铺平了道路，许多图分析任务，如链接预测、推荐和分类，都可以有效地解决[10]，[11]。网络的图形化表现方式揭示了社会生活的各个方面，如交流模式、社区结构和信息扩散[12]，[13]。根据顶点、边和子图的属性，可以将图学习任务分为基于顶点、基于边和基于子图三类。图中顶点之间的关系可以用于分类、风险识别、聚类和社区检测[14]。通过判断图中两个顶点之间的边的存在，我们可以进行推荐和知识推理。基于子图[15]的分类，该图可用于聚合物分类、三维可视化分类等。对于GSP，设计合适的图形采样方法以保持原始图形的特征，从而有效地恢复原始图形[16]具有重要意义。在存在不完整数据[17]的情况下，可以使用图恢复方法构造原始图。然后利用图学习从图数据中学习拓扑结构。综上所述，利用图学习可以解决传统的图分析方法[18]难以解决的以下挑战。