【Google】规范化对概率建模和推理的流（Normalizing Flows for Probabilistic Modeling and Inference）

题目： Normalizing Flows for Probabilistic Modeling and Inference

摘要：

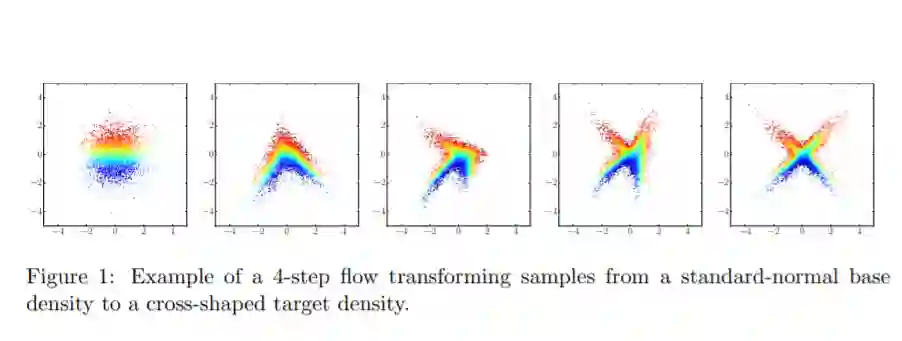
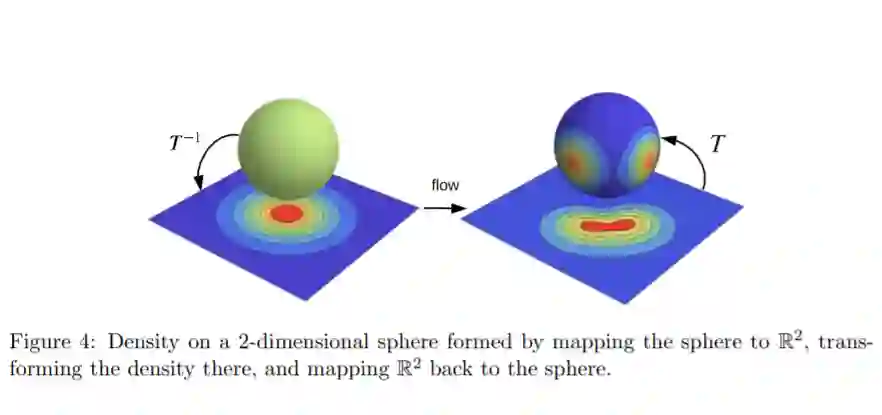
规范化流提供了定义表达性概率分布的一般机制，只需要指定一个(通常是简单的)基本分布和一系列双射转换。最近有很多关于规范化流的工作，从提高它们的表达能力到扩展它们的应用。我们相信这个领域现在已经成熟，需要一个统一的观点。在这篇综述中，我们试图通过概率建模和推理的镜头来描述流，从而提供这样一个视角。我们特别强调流设计的基本原则，并讨论基本主题，如表达能力和计算权衡。我们还通过将它们与更一般的概率转换联系起来，扩展了流的概念框架。最后，我们总结了流在生成式建模、近似推理和监督学习等任务中的应用。

作者简介：

George Papamakarios是伦敦DeepMind的一名研究科学家。之前，在爱丁堡大学(University of Edinburgh)获得了数据科学博士学位，在伦敦帝国理工学院(Imperial College London)获得了高级计算硕士学位。研究兴趣是概率机器学习、贝叶斯推理、深度学习、生成模型和强化学习。

Eric Nalisnick是剑桥大学机器学习小组博士后研究助理，研究兴趣广泛地涉及概率机器学习和统计学。最近一直在研究贝叶斯神经网络的先验，并对深层生成模型进行批判。在加州大学欧文分校的Padhraic Smyth的指导下完成了博士学位。之前，在DeepMind、微软、亚马逊和Twitter做过研究实习。本科在利哈伊大学(伯利恒，宾夕法尼亚州)学习计算机科学和英语文学。