【ICML2025】生成模型中潜空间的Hessian几何结构

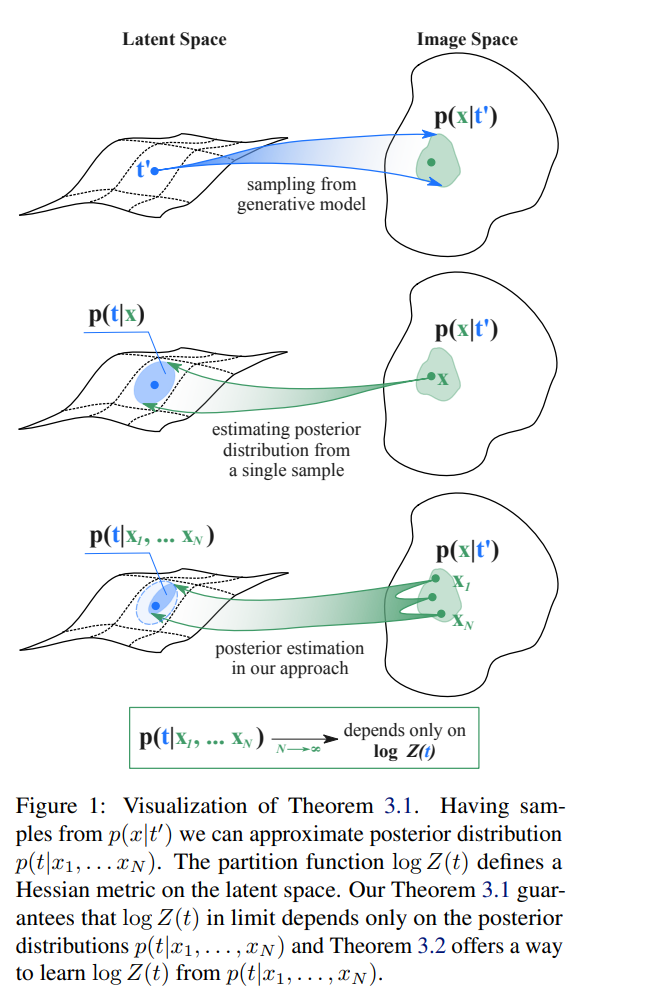
本文提出了一种用于分析生成模型潜空间几何结构的新方法，适用于统计物理模型与扩散模型。该方法通过重构 Fisher 信息度量，来刻画生成模型的潜空间几何。其核心思想是近似生成样本下潜变量的后验分布，并基于此学习对数配分函数，而该函数正是指数族分布中 Fisher 度量的定义基础。 作者为该方法提供了理论收敛性保证，并在 Ising 模型和 TASEP 模型上进行了验证，在重构热力学量方面显著优于现有基线方法。应用于扩散模型时，该方法揭示了潜空间中与相变对应的分形结构，这种结构表现为 Fisher 度量的突变。 研究进一步表明，在单一相态内部，测地线插值近似为线性；但在相变边界处，该线性性被打破，扩散模型在潜空间上的 Lipschitz 常数呈现发散行为。该发现揭示了扩散模型潜空间的复杂结构，并将其与物理中的相变现象建立了联系。

项目代码已开源，地址为：https://github.com/alobashev/hessian-geometry-of-diffusion-models。