【NeurIPS2024】几何轨迹扩散模型

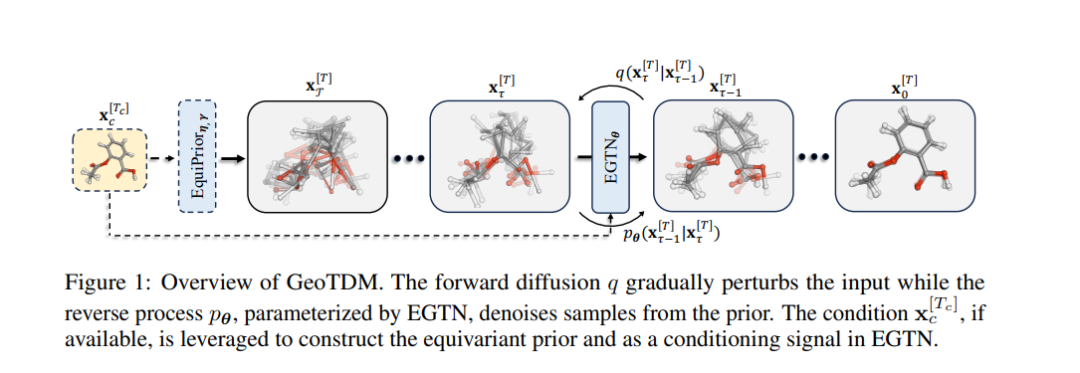
生成模型在生成三维几何系统方面展现了巨大的潜力，这是许多自然科学领域（如分子和蛋白质设计）中的一个基本问题。然而，现有方法仅作用于静态结构，忽视了物理系统本质上是动态的这一事实。在本研究中，我们提出了几何轨迹扩散模型（GeoTDM），这是第一个用于建模三维几何轨迹时间分布的扩散模型。建模这种分布具有挑战性，因为它需要捕捉复杂的空间交互与物理对称性，以及动态中蕴含的时间对应关系。我们从理论上证明了具有等变时间核的扩散模型可以导出具有所需对称性的密度，并开发了一种新颖的转换核，利用SE(3)-等变空间卷积和时间注意力机制。此外，为了在条件生成中引入更具表现力的轨迹分布，我们在前向扩散过程中引入了一种广义可学习几何先验，以增强时间条件。我们在多个场景下进行了广泛的无条件和有条件生成实验，包括物理模拟、分子动力学和行人运动。在广泛的指标上，实验证明GeoTDM可以生成质量显著更高的逼真几何轨迹。