1. 简介

心智理论（ToM）和元推理，正如下文所讨论的，已经成为人工智能（AI）和人-Agent团队的关注领域。两者都有希望通过从人类身上获取灵感，开发出更强大、更有协作性、甚至更像人类的系统。ToM，通过关注他人的心理状态（或其计算机类似物），以及元推理，作为对这些心理状态的一种推理形式。以下两节概述了心智理论（ToM）和元推理，包括在复杂环境中执行多域作战的多人/Agent系统的过去和潜在应用。

2. 心智理论

2.1 人类的心智理论

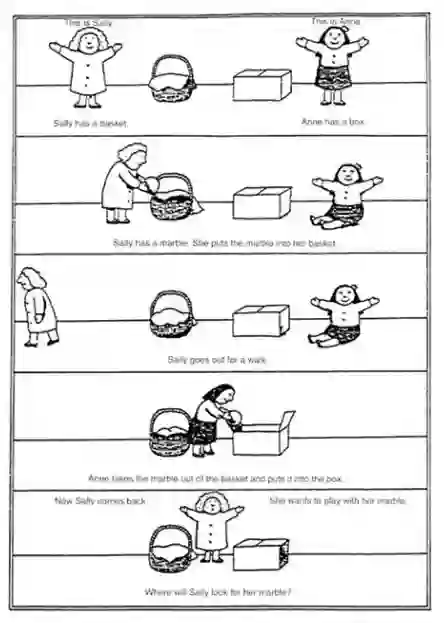
心智理论（ToM）在心理学中描述了人类描绘和推理他人心理状态的能力（Premack and Woodruff 1978）。这方面的一个标志是识别他人错误信念的能力，即一个人使用心智理论来识别世界的状态与另一个人的信念不一致。Sally-Anne测试（Wimmer和Perner，1983年）是评估这种识别错误信念能力的经典任务。在这项任务中，如图1所示，研究对象观看了Sally和Anne的一个场景，Sally把一个物品放在一个地方，然后离开。当Sally离开时，Anne将物品移到一个新的地方。当Sally回来时，被问及她将在何处寻找该物品。如果受试者行使了ToM，他们应该认识到Sally的错误信念，即物品仍然在原来的位置。否则，他们很可能会表明Sally会在物品的实际移动位置上寻找。

图1 通过错误信念任务评估ToM的Sally-Anne任务描述。(Baron-Cohen et al. 1985)。

像Sally-Anne任务这样的任务已经被用来表明，在年幼的儿童（Wellman等人，2001年）、自闭症患者（Baron-Cohen等人，1985年）和非人类动物中，ToM是不准确的或不可用的。然而，非陈述性任务（如Sally-Anne任务中不需要明确的答案，但可以测量，例如，看时间或第一次看场景中的位置）表明，这种类型的推理在较小的年龄，甚至在非人灵长类动物和鸟类中都是可用的（Baillargeon等人，2010；Horschler等人，2020；Hampton 2021）。研究人员还强调了测试中不确定性和互动性的重要性，在研究参与者和推理对象之间有更大的不确定性和知识不对称的环境中，以及在参与者和推理对象之间有更多互动的测试中，ToM更可能得到锻炼（Rusch等人，2020）。相反，如果ToM测试不包含足够的不确定性或知识不对称，则可能无法在其他环境中确实表现出ToM的参与者身上找到证据，大概是因为它们没有充分促使参与者考虑另一个人的观点。

最后，正如Blaha等人（2022）所强调的，那些能够在测试中表现出ToM证据的人，在现实世界的互动中往往不会有同样的表现。在一个交流游戏中，Keysar等人（2003）发现，神经正常的成年参与者在得到指导者的指示时，会表现得好像指导者拥有准确的知识，而他们（指导者）却已知缺乏甚至持有错误的信念。同样，Bryant等人（2013年）在一天中随机抽样评估了参与者在什么情况下考虑他人的心理状态的频率，他们发现参与者很少考虑心理状态，在社会交往中比独处时更少考虑心理状态，此外，比起其他人，他们更可能考虑自己的心理状态。这些结果表明，成年人可能会发现社会交往对认知的负担太重，而无法在即时考虑他人的心理状态时采用ToM。

2.2 人类心智理论的建模

对ToM进行计算建模通常是为了开发和测试ToM的认知理论，同时也是为了让我们建立能够与人类用户进行更自然和有效的互动的技术。这一领域的许多研究表明，贝叶斯模型可以提供令人印象深刻的ToM近似值（Baker等人，2017年；Csibra，2017年；关于应用贝叶斯推理的博弈论和K级思维方法，也请参见Yoshida等人，2008年和Robalino和Robson，2012年）。

这种贝叶斯推断通常是通过反强化学习（IRL）进行的。正如Jara-Ettinger（2019）所描述的，"预测其他人的行为是通过模拟具有假设的信念和欲望的RL模型来实现的，而心理状态推断则是通过反转这个模型来实现的"（p. 105），研究发现，"在简单的二维显示中，通过贝叶斯推理的IRL在推断人们的目标[Baker等人，2009]、信念[Baker等人，2017]、欲望[Jern等人，2017]和帮助性[Ullman等人，2009]时产生类似人类的判断"（p.105）。然而，反向贝叶斯推理需要强大的先验因素才能成功（Baker等人，2009）。虽然人类似乎也采用了强大的先验，虽然这些先验在新情况下可能并不总是很合理的，但它们至少在模型中是相当透明的。

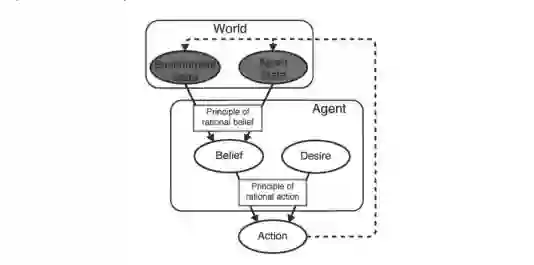
作为IRL的一部分，部分可观察的马尔科夫决策过程（POMDPs）已被有效地用于模拟人类的ToM，其中Agent的行动在环境中是可观察的，但他们的信念和目标必须通过近似理性假设的逆向规划来推断。如图2所示，这种模型已被证明可以提供与人类相媲美的判断（Baker，2012）。例如，在Baker（2012）的研究中，人类参与者+POMDP模型观察了一个模拟的Agent在一个简单的有遮挡的地形上导航，以选择购买午餐的餐车，然后他们被要求对Agent的目标（即首选餐车）提供判断。在这种情况下，允许改变目标的模型的判断结果与人类的判断密切相关，而且比不允许改变目标或允许目标包括子目标的类似模型更好。这些结果表明，这样的模型可以人为地接近人类的判断，甚至可以被人类推理者使用。

图2 Baker（2012）假设的ToM因果图，其中观察到的（灰色）信息影响Agent的（未观察到的）信念、欲望和最终的行动，并以理性为中介。(图片经许可改编自Baker [2012]。)

类似的工作已经探索了更复杂的推理环境，例如使用元贝叶斯框架来模拟不同信任度条件下的人类ToM（Diaconescu等人，2014）。参与者玩了一个经济游戏，他们得到了（真实的、非社会的）概率信息，以帮助他们在二元彩票中做出选择，他们还得到了一个顾问的（社会的）信息，这个顾问帮助玩家的激励是不同的。人类的结果最好由一个层次模型来模拟，该模型可以为社会和非社会信息分配不同的权重，并允许根据过去表现的动态估计来推断顾问不断变化的目标。虽然这项工作和其他（例如Meinhardt-Injac等人，2018年）工作已经探讨了人类使用社会与非社会来源的线索进行推断，但研究似乎没有对涉及更多不确定信息来源的ToM以及人类如何优先考虑和纳入决策过程进行建模。

这些类型的ToM模型表明，消减模型的部分内容是可能的，而且结果是可以预测的。例如，如果人类在推理他人时使用贝叶斯先验，并且我们根据经验更新这些先验，可能有一些人无法有效地更新先验。事实上，这可能是精神分裂症的情况，人们对他人持有特别消极和怀疑的看法，而这些看法并没有通过积极的互动得到改善。另一方面，自闭症可能代表了整个ToM机制更普遍的消融（访问），因为自闭症患者在ToM的测试中往往表现不佳（TEDx Talks 2014；Prevost等人2015）。

2.3 机器的心智理论

计算性ToM也不是用来直接模拟人类的推理，而是作为一个框架，让Agent对其他Agent进行推理。此外，这样的Agent可能更容易解释，并促使更好的人与Agent的互动。ToM可以让Agent甚至在遇到其他Agent之前就持有关于他们适当的先验，更新关于他们的信念，并识别他们的错误信念。

这在Rabinowitz等人（2018）中得到了说明，在那里，模型学会了通过根据它们过去的行为预测它们的未来行为来识别不同种类的Agent（例如，一个物种倾向于追求附近的物体而不是遥远的物体）。值得注意的是，这项工作包括一项假想任务，即一个视力有限的Agent观察其最终目标物体，当它首先追求一个子目标物体时，该物体在Agent的视线内或视线外概率性地改变位置。观察到Agent在未观察到移动时比在观察到移动时更频繁地在其原始位置追踪最终目标对象。这表明，该模型学会了将其对环境的全部知识与Agent的有限知识分开，使其能够识别Agent的错误信念。

2.4 人类和机器之间的心智理论

当人类能够对机器的 "思想状态 "做出准确推断时，很可能会提高信任度和性能。这已经成为可解释人工智能领域内提高信任和性能的动力（Akula等人，2019）。同样，随着机器能够更准确地推断出人类的意图，它们的效用会增加，并进一步获得信任（Winfield 2018）。

3. 元推理（Metareasoning）

元推理是一个通用的人工智能术语，指的是在计算系统中 "思考问题 "。推理算法被用来做决策，而元推理算法被用来控制推理算法或在一组推理算法中进行选择，决定在不同情况下应该使用哪种决策方法（Cox and Raja 2011）。元推理的一个经典例子是确定推理算法在特定情况下应该停止还是继续（例如，Carlin 2012）。

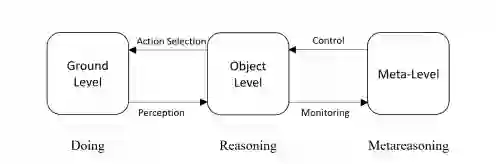
元推理可以被描述为图3，其中推理发生在目标层，基于应用层的观察，在目标层做出的决策在应用层被制定。例如，当目标层的算法从传感器输入中确定有入侵者存在时，感应式警报可能会在应用层响起（例如，当在10秒内检测到两个或多个运动事件时，该算法可能会响起警报）。当来自目标层的信息在元层被观察和改变时，元推理就发生了。在前面的例子中，如果警报被频繁触发，元层的算法可能会调整警报的灵敏度，导致系列问题（例如，这个元层的算法可能会在目标层施加一个新的算法，只有在10秒内检测到三个或更多的运动事件时才会发出警报）。

图3 元推理的经典决策-行动循环图，推理发生在目标层面，以选择将发生在应用层的行动，而元推理发生在元层面，以控制发生在目标层面的行动。

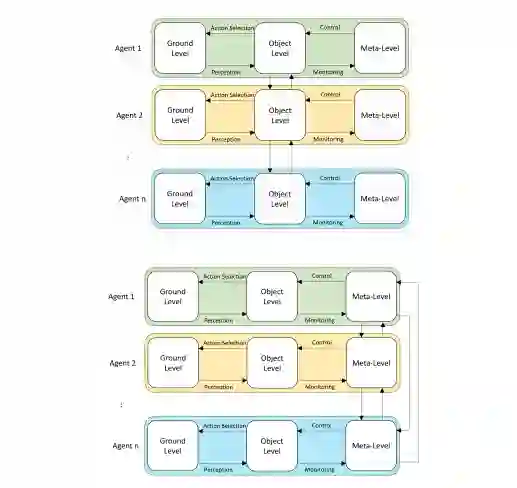
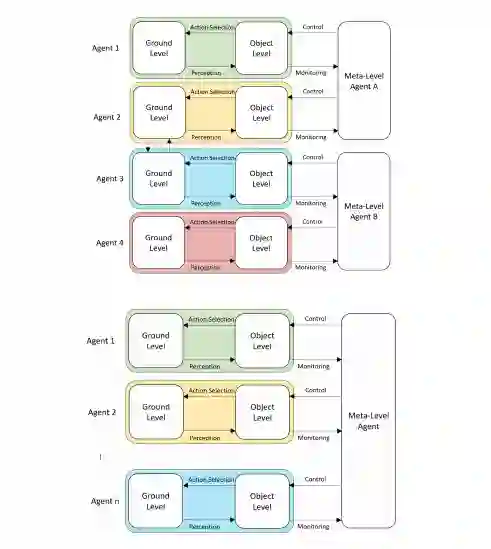
元推理可以发生在一个单一的Agent中，如图3所示，也可以发生在一个多Agent系统（MAS）中（图4）。元推理经常被用于多Agent的环境中，以优化整个系统的性能，而且有许多选项可以选择如何实现它，对时间和计算能力等资源产生不同的影响。例如，MAS中的Agent可以独立地执行它们的元推理，并在目标层进行通信，当通信成本高且协调是低优先级时，这可能是一个好的解决方案。当协调更为重要时，独立进行元推理的Agent可以在元层进行通信，以共同确定它们将如何独立进行元推理（Langlois等人，2020）。

图4（上图）一个MAS系统，每个Agent的元推理都是独立发生的。(下图）一个MAS系统，每个Agent的元推理与其他Agent的元推理进行交流和协调。(图示来自Langlois等人[2020]，经许可。)

元推理也可以由独立的元推理Agent以更集中的方式进行（图5，顶部）。在通信资源允许的情况下，最好的协调和元推理预计将来自一个集中的元推理Agent（图5，下）（Langlois等人，2020）。

图5（上图）一个有多个独立的元推理Agent的MAS。(下图)一个拥有单一集中式元推理Agent的MAS。(图示来自Langlois等人[2020]，经许可。)

系统在其元推理的目标上也有所不同。如本节开篇所述，单Agent元推理通常用于控制算法的停止或切换，并应用于各种领域，包括调度和规划（如Lin等人，2015）、启发式搜索（Gu 2021）和目标检测（如Parashar和Goel 2021）。在MAS中，元推理经常被用来控制系统内的通信和资源，包括控制通信频率或内容，或分配任务（Herrmann 2020）。

在元推理中的另一个问题是，有多少学习或元推理应该在线上与线下发生。因为在线元推理在时间和计算上可能是昂贵的，所以离线策略通常在不过度损害系统准确性的范围内被最大化（例如，Carrillo等人，2020）。

广义上讲，ToM是一种元推理的形式，或者说是 "关于思考的思考"。然而，如图3所述，元推理是通过监测和控制目标层来进行的，而ToM涉及从应用层发生的事情进行推理，而不直接进入目标层（例如，Agent的信念）。

4. 结论

虽然元推理已经被广泛用于单实体和多实体系统以提高性能，但ToM方法可以说还没有被作为一种提高人工智能Agent性能的方法进行深入探讨。这几乎可以肯定的是，部分原因是ToM与人类的认知有更紧密的联系，这对合理的ToM模型有很强的限制，并使研究偏向于人类的应用。此外，ToM本身仍有一些争议（例如，谁拥有它？它是什么时候获得的？在什么条件下行使？）但它为创建更透明（如果不是真实的人类）的系统带来了希望，特别是用多个信息源和不同的出处和确定性进行推理的系统。特别是最近的计算性ToM方法，它使用更简单的、启发式的ToM定义（例如，Rabinowitz等人，2018），可能是这个领域创新的最佳来源。

成为VIP会员查看完整内容