【伯克利博士论文】不确定性序列决策:最优性保证，组合学习，以及在机器人技术和生态学中的应用，256页pdf

不确定性条件下的序列决策问题通常涉及部分可观察的马尔可夫决策过程（POMDPs）。POMDPs 数学上捕捉了在每一步考虑潜在奖励和未来可能遇到的不确定性时的决策制定，使得它们成为许多现实世界问题的理想和灵活的表示。然而，这类带有各种不确定性源的序列决策问题非常难以解决，特别是当状态和观察空间是连续的或混合的，这在物理系统中往往是常见的情况。此外，现代问题设置需要复杂的机器学习技术来有效处理像图像、文本或音频输入这样的复杂数据结构，同时执行如利用噪声相机图像进行定位或预测其他代理的意图和位置等复杂的推理。涉及人工智能和机器学习方法的现代方法提供了强大的计算资源，可以有效地管理上述挑战。许多这些决策制定算法和机器学习技术可以捕获严格的理论保证或实证性能，但很少有能同时捕获两者的。

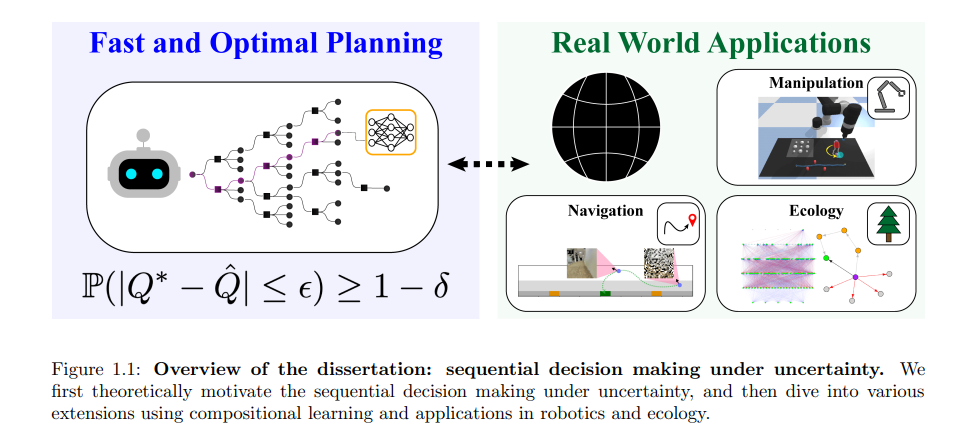
这篇博士论文旨在从多个角度研究不确定性下的序列决策制定：理论保证，与学习的整合，以及现实世界的应用。我们在 POMDPs 的基础框架的数学分析，以及通过组合学习与机器学习技术的整合来启用和部署这些技术之间找到了平衡。我们首先通过分析新颖的 POMDP 解算器及其理论收敛性质开始论文的理论部分。这部分介绍了几种新颖的 POMDP 算法，这些算法为研究处理连续观察和行动空间的现代 POMDP 算法的收敛性质提供了基础。然后，我们覆盖了一个更一般的结果，该结果为解决 POMDPs 的粒子信念近似问题提供了理论保证和理由，同时在原始 POMDP 中保留了保证。这个结果正式证明了一种常见的 POMDP 近似技术，即粒子似然权重，这是第一种在理论上解释使用这种技术的现代 POMDP 算法家族的方法。

然后，我们介绍了通过组合学习将基于模型的规划与基于学习的组件整合在一起的方法，以适应现实世界的机器人设置。首先，我们研究如何通过使用深度生成模型将上述 POMDP 规划算法与机器学习组件整合，使这些算法能够处理视觉导航任务。其次，我们通过使用示范序列和加权的多任务学习来对桌面操作的机器人臂操控算法进行大幅扩展。最后，我们提出了序列决策制定在生态学社区状态导航子领域的新应用领域。具体来说，我们专注于将物种共存导航问题构建为最优路径规划问题。这种方法使我们能够通过分析对平衡状态的小扰动来理解种群动态，然后找到允许有效导航的行动序列。我们还讨论了将序列决策制定框架应用于社区状态导航问题及其外的好处和影响。然后，我们再次总结主要贡献，并将新的贡献置于上下文中。我们还讨论了在不确定性下的序列决策制定方面的未来工作机会，包括新的理论发展、组合学习的替代方法以及对现实世界应用产生重大影响的其他途径。

1. 引言

这篇论文基于不确定性下的顺序决策制定的理念，最常见的是处理部分可观察的马尔科夫决策过程（POMDPs），这是一种通用的形式化方法，可以代表许多这种不确定性下的顺序决策制定问题。POMDPs数学上捕获了在每一步做出决策的挑战，同时考虑到代理可能在未来遇到的潜在奖励和不确定性。因此，不确定性下的序列决策制定问题要求代理理解可能以多种形式出现的不确定性：在采取某种行动后，系统在下一步将如何演变？代理如何从环境提供的嘈杂或不完整的信息中提取有关我们当前位置或配置的信息？完成任务的最佳行动是什么，同时如何将失败风险降至最低？

随着现代问题设定在环境设置（如处理图像、文本或音频输入）和推理（如使用噪声相机读数进行导航或预测社区状态演变）方面变得极其复杂，决策方法能够适应推理和最终解决这些问题就显得至关重要。虽然现代技术如人工智能和机器学习方法提供了处理这些问题的强大工具，但重要的是要提供一定程度的性能保证和保障，以便在许多实际应用中发挥作用。不幸的是，许多决策制定解决器和系统达到了实证性能或理论保证，但很少同时捕获这两者。由于这些技术及其应用的复杂性，同时数学地表示和正式地证明许多现代机器学习技术及其在顺序决策制定中的应用变得极其困难。本文试图在数学上证明POMDPs的基础框架，和使这些技术能够以一种尽可能保持享有这些保证的系统结构的方式与机器学习技术相结合之间找到平衡。本质上，不仅决策方法的有限样本最优性保证的理论基础是重要的，而且这些方法应通过与现代机器学习和人工智能技术的整合，使其能够应用于更真实的问题领域，包括机器人技术和生态学。在这个意义上，组合学习的方法在理论严谨性和计算能力之间取得了极好的平衡：问题结构和领域知识的先验知识被提炼成一个适当的顺序决策问题，其中模型组件通过启用这些组件的单个和/或同时学习得到加强。因此，这篇论文的核心哲学是：为了让快速和最优的不确定性下的顺序决策方法在实际应用中发挥作用，它们应该通过数学证明和保证得到严格的基础，并通过与现代技术的整合得到增强。

因此，我们的目标是设计出在形式上理论上得到很好证明的解决方案和系统，通常以统计保证的形式，同时在计算上高效且准确。在这些框架的指导下，我们还在寻找顺序决策框架可能在以前探索不足的应用领域中有用的方式，特别是关于物种共存导航的生态问题。

这篇论文从理论、计算和实际应用三个不同的角度探讨了不确定性下的决策制定主题。在第一部分的第2章和第3章，我们将介绍理解这篇论文中的想法所必需的数学背景，并提供额外的材料，涵盖了该领域一些最近的发展。接下来的部分和章节概述了从三个不同角度解决不确定性下的顺序决策制定主题的关键贡献。由于这篇论文也作为作者以前发布的作品的汇编，我们用一个概述章节介绍每一个主要部分，简明地概述了主要贡献是什么，为什么它们重要，以及它们如何融入到研究不确定性下的顺序决策制定的整体叙述中。