张量神经网络是什么？香港城市大学最新《张量网络与神经网络结合》综述

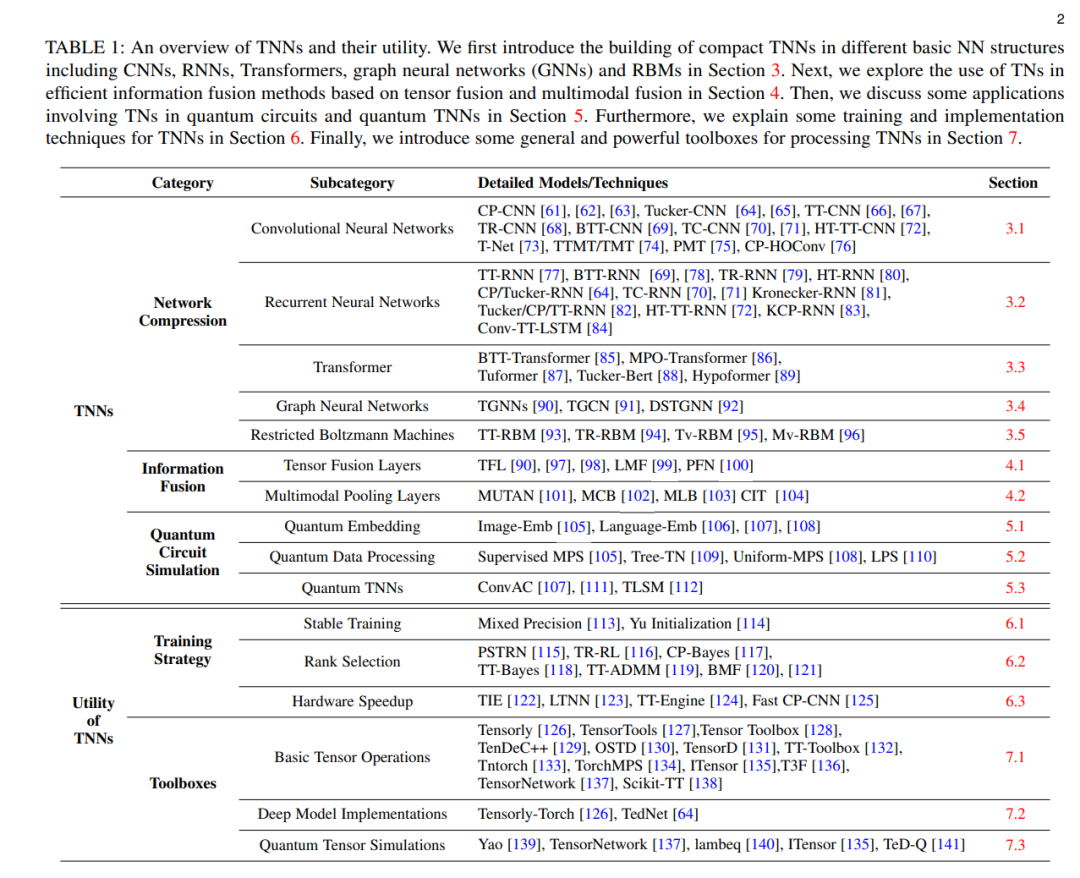
张量网络(TNs)和神经网络(NNs)是两种基本的数据建模方法。TNs通过将指数维数转换为多项式复杂度，被提出作为大规模张量面临的维数灾难的解决方案。因此，它们吸引了量子物理和机器学习领域的许多研究。另一方面，神经网络是受构成人类大脑的生物神经网络启发的计算系统。近年来，神经网络及其变体在计算机视觉、自然语言处理和机器人研究等各种应用中取得了卓越的性能。有趣的是，尽管这两种类型的网络来自不同的观察，但它们通过TNs和NNs共同的内在多线性结构不可避免地联系在一起。因此，出现了大量关于TNs和NN结合的思想火花。将"张量网络与神经网络"的组合称为张量神经网络(tensorial neural networks, TNNs)。**本文从三个方面对TNNs进行了介绍。1)网络压缩。TNs可以大大减少神经网络中的参数，满足构造有效神经网络的思想。2)信息融合。TNs可以自然有效地增强神经网络的能力，对多种模态、视图或各种数据来源之间的相互作用进行建模。3)量子电路仿真。**TNs可以帮助设计和模拟量子神经网络(QNNs)。本综述还研究了改进TNN的方法，研究了用于实现TNN的有用工具箱，并试图记录TNN的发展并强调其潜在的未来方向。据我们所知，这是第一次将神经网络、TNs和量子电路之间的联系联系起来的全面综述。我们在https://github.com/tnbar/awesome-tensorial-neural-networks上提供了一个精心策划的TNNs列表。

1. 引言

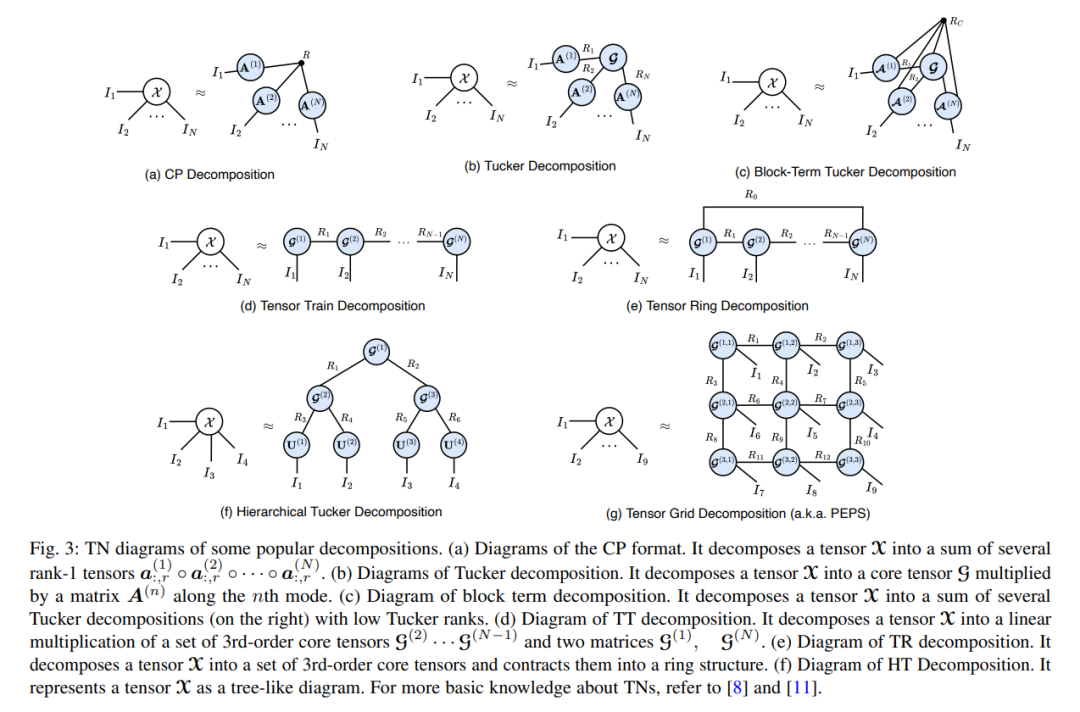
**张量是高阶数组，表示多个模态源之间的多方向相互作用。**相比之下，向量(即一阶张量)和矩阵(即二阶张量)分别只能以一种或两种模式访问。张量作为一种常见的数据类型，在[1]，[2]，[3]，[4]等场景中得到了广泛的观察。例如，功能磁共振成像(fMRI)样本本质上是四阶张量，由随时间变化的三维体素组成[5]，[6]，[7]。在量子物理中，用于研究多体量子系统的变分波函数也是高阶张量[8]，[9]。对于时空交通分析，几周内从多条道路收集的道路流量/速度信息也可以构建为一个三阶张量(road segment×day×time of day)[10]。然而，对于高阶张量，当模态数量增加时，张量中的元素总数呈指数增长，导致存储和处理张量时出现灾难。这种现象也被公认为“维数诅咒”[11]。 张量网络(TNs)。TNs[8]，[11]，[12]通常是通过张量收缩连接的小尺度张量的可数集合。这些小尺度张量被称为“分量”、“块”、“因子”或“核心”。非常大规模的张量可以通过TNs以极度压缩和分布式的格式近似表示。因此，对以前无法处理的高阶张量进行分布式存储和高效处理是可行的。通过TN方法，可以缓解或完全克服[11]的维数灾难问题。常用的TN格式包括CANDECOMP/PARAFAC (CP)[13]、[14]、[15]、Tucker分解[16]、[17]、Blockterm Tucker (BTT)分解[18]、[19]、[20]、矩阵积态(MPS)/张量列(TT)分解[21]、[22]、[23]、[24]、矩阵积算子(MPO)/矩阵张量列(mTT)分解[21]、[22]、[23]、[24]、张量环(TR)分解[25]、树TN/层次Tucker (HT)分解[26]、投影纠缠对态(PEPS)/张量网格分解[8]、[27]，[28]，多尺度纠缠重整化[29]等。为了理解TNs相互关联的结构，TN图被开发为一种简单的图形图(将在2.2节讨论)。TN可以为分析一些计算上不可接受的任务提供一个理论和计算框架。例如，Pan等人基于TNs的低秩结构，[30]能够在15小时内使用512个图形处理器(GPU)解决量子随机电路采样问题;这个问题之前被认为在最强大的经典电子超级计算机上需要超过10000年的时间，并有效地挑战了谷歌的量子计算机“Sycamore”的量子霸权。其他应用包括脑分析[31]、量子化学计算[32]、人脸聚类[33]、降维[34]、缺失值估计[35]、潜在因子分析[36]、子空间学习[37]等。

**神经网络(NNs)。**神经网络是受生物启发的学习范式，使机器能够通过反向传播从观察数据中学习知识[38]，[39]。多层堆叠的神经网络，即深度神经网络[40]、[41]，因其强大的从深层结构中捕获丰富信息的能力，被广泛应用于人工智能领域。典型的DNN类型包括受限玻尔兹曼机(RBMs)[42]、卷积神经网络(CNNs)[41]、[43]、循环神经网络(RNNs)[44]、[45]和transformer[46]、[47]。DNNs目前在计算机视觉[48]和自然语言处理[49]的广泛应用中达到了最先进的性能。例如，一些CNN架构，如AlexNet [50]， VGGNet [51]， GoogLeNet[52]和ResNet[53]在ImageNet数据集[54]上赢得了冠军，展示了解决图像分类任务的良好潜力。特别是Alphafold[55]，[56]，这是一种Transformer架构，可以在几天内识别蛋白质的结构，此前研究人员需要数年时间。最近，Alphafold2[55]、[56]以平均原子精度预测了几乎所有已知蛋白质的结构。深度学习技术仍在推动多个学科的发展，包括语音识别[57]、DNA突变检测[58]、结构生物学[55]、[56]、药物发现[59]、食品安全[60]等。

**张量网络遇见神经网络。如上所述，TNs和NN是两种来自不同起源并在不同方面取得成功的网络。有趣的是，它们通过它们的多线性数学性质紧密结合而不是相互正交[11]。因此，一种有希望的方法是通过多元线性来整合它们，以达到“整体大于部分的总和”的目标。TNs的主要优点是其紧凑的结构、多条目以及与量子力学的密切联系，而NN则以其广泛的应用而闻名[8]，[12]。基于这些观察，可以通过三种方式将TNs和NNs结合起来。(1)网络压缩。**神经网络在各种任务中取得了许多成功[40]，[41]，[41]。然而，神经网络仍然存在大量维度的过度线性乘积计算和维数灾难[78]。解决这个问题的一个有希望的解决方案是利用TNs的轻量级和多线性特性[68]，[78]，[79]。其中，TNs可以将NNs的任何张量分解为更小的块，从而将维度降低到线性复杂度[61]，[62]。例如，与使用朴素长短期记忆网络(LSTM)进行动作识别任务相比，利用TN技术分解权重张量的TR-LSTM[79]模型可以将参数数量压缩约34000倍，同时性能优于朴素LSTM。 **(2)信息融合。**在实际的数据分析中，多模态数据的高阶交互建模对于获得更好的性能是很重要的。然而，神经网络通常用于处理单模向量的输入，因此它们缺乏足够的表达能力来建模这种高阶交互[101]。为了解决这个问题，一种有希望的方法是将TNs嵌入到神经网络中，作为有效的融合单元，借助多入口属性[97]，[98]，[100]来处理多模态数据。以视觉问答(VQA)任务[142]为例，多模态Tucker融合(MUTAN)[101]可以通过Tucker格式框架学习文本表示和视觉表示之间的高级交互。因此，MUTAN通过有效的参数化低秩结构实现了最先进的性能。(3)量子电路仿真。TNs可以作为仿真器，成为经典神经网络和量子电路之间的桥梁。首先，许多研究建议在量子电路上实现神经网络，以通过量子计算方案的超并行性来加快其运行速度[143]，[144]。然而，目前量子计算机还没有足够的能力直接部署神经网络，这给验证量子神经网络(quantum neural networks, QNNs)的可能性能带来了困难[143]。幸运的是，由于TNs和量子电路[8]之间的等效性，[145]，TNs可以成为电子计算机中有效的量子模拟器。详细地说，量子电路中的输入量子比特和幺正运算门可以看作张量。门连接也可以被视为TN方案中的张量收缩[145]。利用TNs实现NNs的量子电路模拟，可以在制造出真正强大的量子计算机之前，开启QNNs探索的新时代。

我们将这种连接TNs和NNs的方法族称为张量神经网络(TNNs)。据我们所知，这是第一次将神经网络、TNs和量子电路之间的联系联系起来的全面综述。TNN及其效用的概述如表1所示。本综述的其余部分组织如下。第2节提供了张量符号、张量图和TN格式的基础知识。第3节讨论如何使用TNs来构建紧凑的TNN。第4节探讨了使用TNN的高效信息融合过程。第5节讨论了TNs在量子电路和TNNs中的一些基本应用。第6节解释了TNNs的一些训练和实现技术。第7节介绍了可用于处理TNN的通用而强大的工具箱。