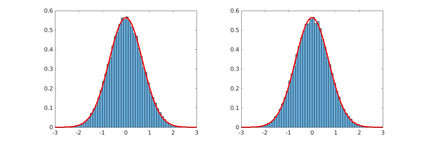
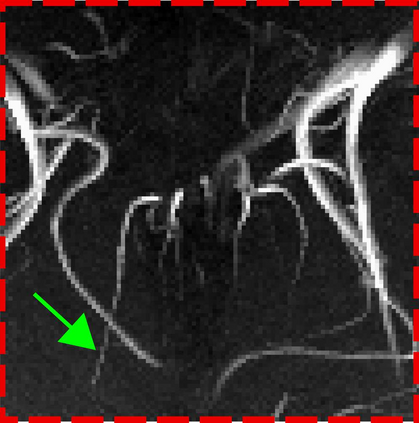
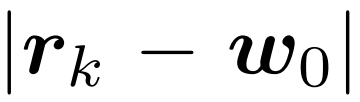Magnetic Resonance Imaging (MRI) has excellent soft tissue contrast but is hindered by an inherently slow data acquisition process. Compressed sensing, which reconstructs sparse signals from incoherently sampled data, has been widely applied to accelerate MRI acquisitions. Compressed sensing MRI requires one or more model parameters to be tuned, which is usually done by hand, giving sub-optimal tuning in general. To address this issue, we build on previous work by the authors on the single-coil Variable Density Approximate Message Passing (VDAMP) algorithm, extending the framework to multiple receiver coils to propose the Parallel VDAMP (P-VDAMP) algorithm. For Bernoulli random variable density sampling, P-VDAMP obeys a "state evolution", where the intermediate per-iteration image estimate is distributed according to the ground truth corrupted by a zero-mean Gaussian vector with approximately known covariance. To our knowledge, P-VDAMP is the first algorithm for multi-coil MRI data that obeys a state evolution with accurately tracked parameters. We leverage state evolution to automatically tune sparse parameters on-the-fly with Stein's Unbiased Risk Estimate (SURE). P-VDAMP is evaluated on brain, knee and angiogram datasets and compared with four variants of the Fast Iterative Shrinkage-Thresholding algorithm (FISTA), including two tuning-free variants from the literature. The proposed method is found to have a similar reconstruction quality and time to convergence as FISTA with an optimally tuned sparse weighting and offers substantial robustness and reconstruction quality improvements over competing tuning-free methods.
翻译:磁共振成像( MRI) 具有极好的软组织对比, 但却受到一个内在缓慢的数据采集过程的阻碍。 压缩的感测, 重建了来自不连贯抽样数据的微弱信号, 被广泛用于加速MRI的获取。 压缩的感测磁共振需要一种或多种模型参数来调整, 通常通过手动进行, 并进行一般的亚最佳调试。 为了解决这个问题, 我们以作者以前关于单层流体自由变异调调频传递信息( VDAMP) 算法( VDAMP) 的计算法为基础, 将框架扩展至多个接收器螺旋, 以提议平行的 VDAMP (P- VDAMMP) 算法。 对于Bernoulli 随机随机随机随机的密度取样, P- VDAM 执行一个“ 状态变异性”, 中间值图像估测算法被零度高度的高度矢量变异性。 据我们所知, P- VDAM 是在多层流流数据中找到的第一个算算法, 符合州变异性变异性变异性数据, 和大脑变异性变异性变异性变数, 我们利用了一种动态变压的变压法, 将风险变压的变压数据 向向向 。