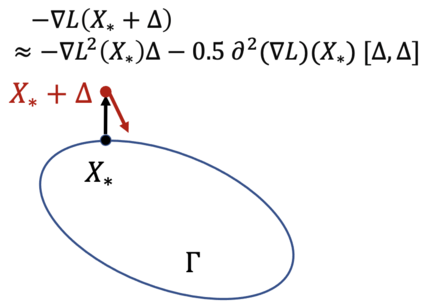
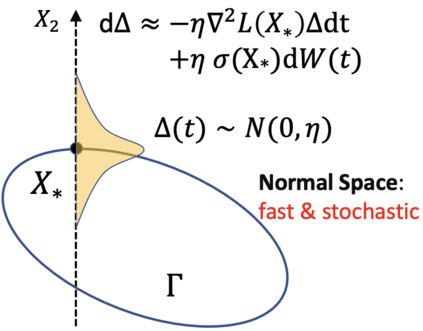
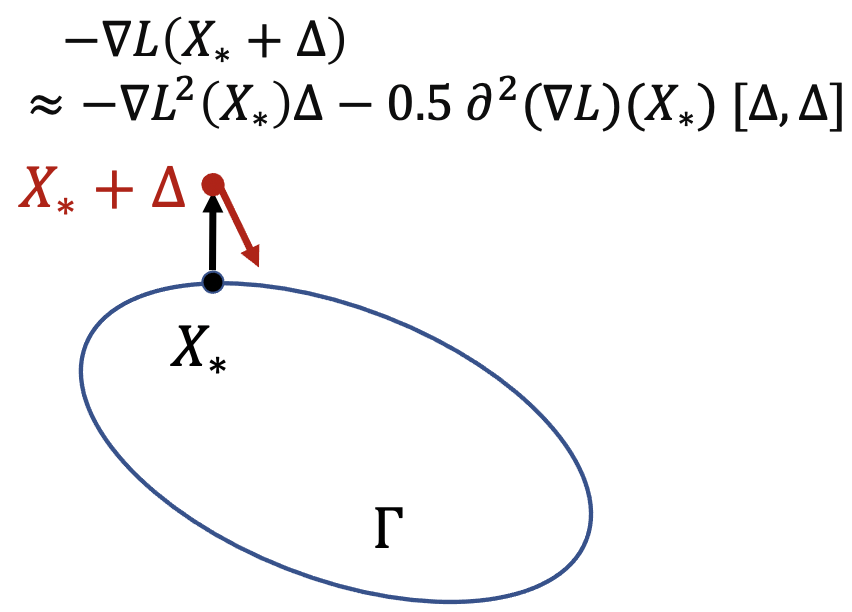
Understanding the implicit bias of Stochastic Gradient Descent (SGD) is one of the key challenges in deep learning, especially for overparametrized models, where the local minimizers of the loss function $L$ can form a manifold. Intuitively, with a sufficiently small learning rate $\eta$, SGD tracks Gradient Descent (GD) until it gets close to such manifold, where the gradient noise prevents further convergence. In such a regime, Blanc et al. (2020) proved that SGD with label noise locally decreases a regularizer-like term, the sharpness of loss, $\mathrm{tr}[\nabla^2 L]$. The current paper gives a general framework for such analysis by adapting ideas from Katzenberger (1991). It allows in principle a complete characterization for the regularization effect of SGD around such manifold -- i.e., the "implicit bias" -- using a stochastic differential equation (SDE) describing the limiting dynamics of the parameters, which is determined jointly by the loss function and the noise covariance. This yields some new results: (1) a global analysis of the implicit bias valid for $\eta^{-2}$ steps, in contrast to the local analysis of Blanc et al. (2020) that is only valid for $\eta^{-1.6}$ steps and (2) allowing arbitrary noise covariance. As an application, we show with arbitrary large initialization, label noise SGD can always escape the kernel regime and only requires $O(\kappa\ln d)$ samples for learning an $\kappa$-sparse overparametrized linear model in $\mathbb{R}^d$ (Woodworth et al., 2020), while GD initialized in the kernel regime requires $\Omega(d)$ samples. This upper bound is minimax optimal and improves the previous $\tilde{O}(\kappa^2)$ upper bound (HaoChen et al., 2020).
翻译:理解 Stochastic Gradientle Group (SGD) 的隐含偏差是深层学习中的关键挑战之一, 特别是对于超平衡化模型来说, 当地损失最小化者可以形成一个元体。 直观地, 学习率足够小的美元( 美元), SGD 跟踪 梯度源( GD), 直到它接近这样的元体, 梯度噪音阻止进一步趋同。 在这样一个制度中, Blanc 等人 (2020) 证明, 标签噪音的SGD 本地标准降低了一个定期值( 定期值), 损耗的锐度, $mathrm{ tr} [\ nabla2L] 。 本文为这种分析提供了一个总体框架, 调整了来自 Katzenberger (1991) 的想法。 它原则上可以完全描述 SGDGD( amdic) 的整形偏差值( SDE), 描述参数的动态的动态, 由损失函数和噪变调调调 美元( 美元) 开始, 美元) 开始分析, 美元 开始的 需要 直值 直值 直值 。