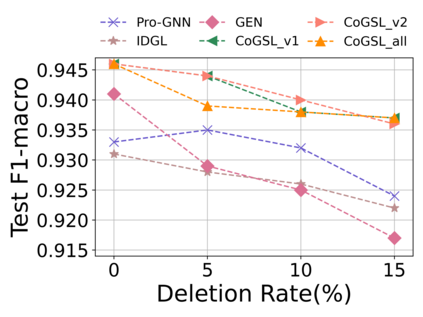
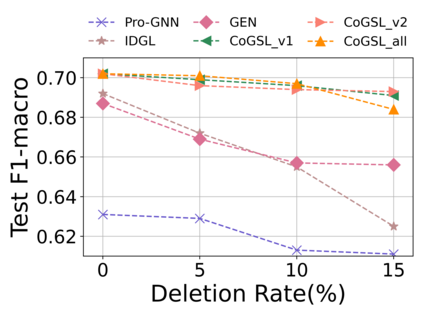
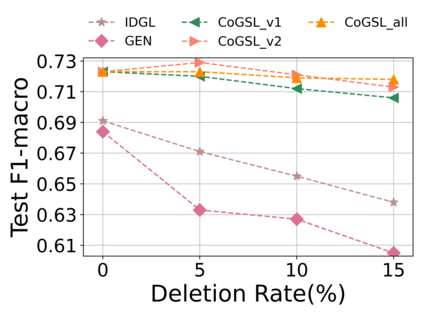
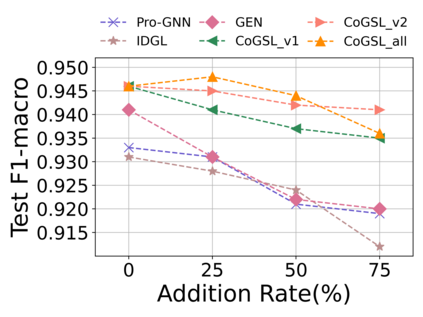
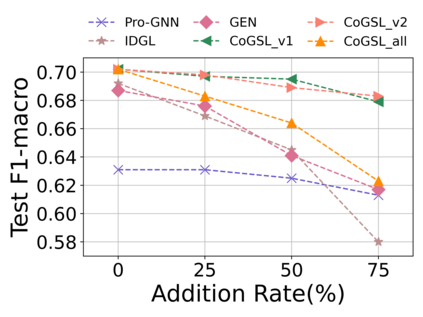
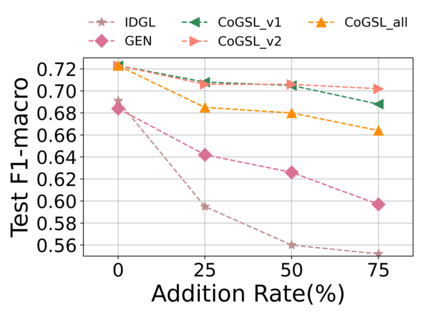
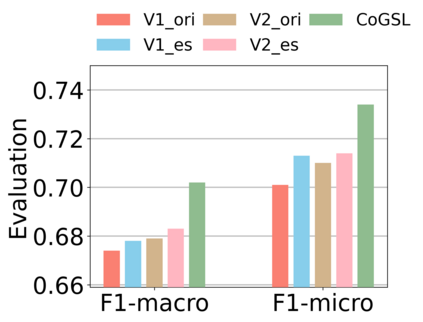
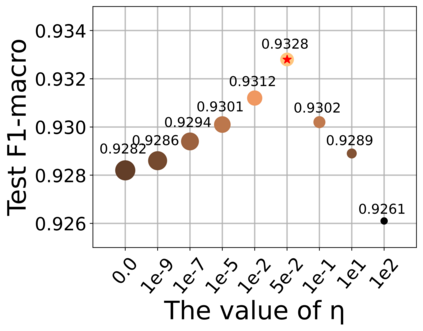
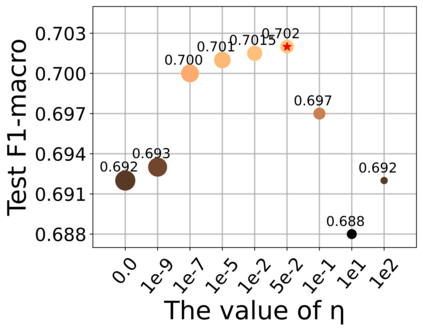
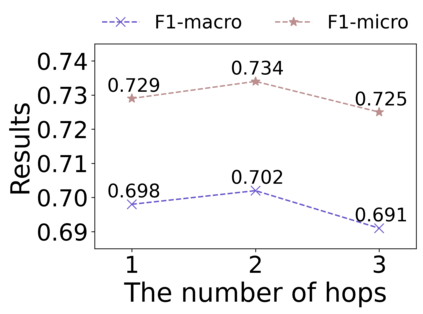
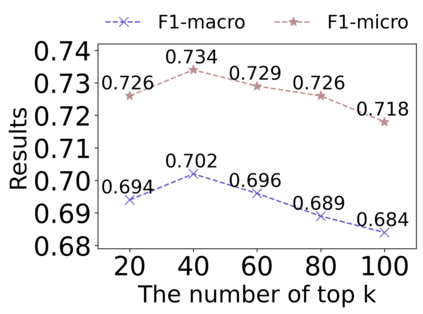
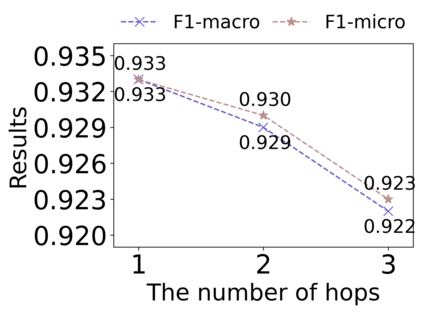
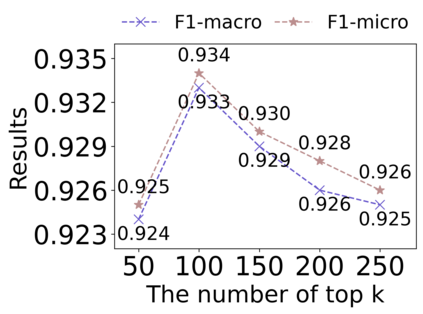
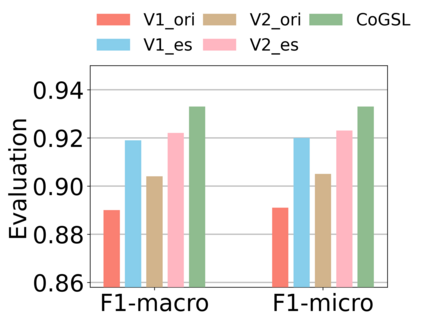
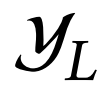Graph Structure Learning (GSL) recently has attracted considerable attentions in its capacity of optimizing graph structure as well as learning suitable parameters of Graph Neural Networks (GNNs) simultaneously. Current GSL methods mainly learn an optimal graph structure (final view) from single or multiple information sources (basic views), however the theoretical guidance on what is the optimal graph structure is still unexplored. In essence, an optimal graph structure should only contain the information about tasks while compress redundant noise as much as possible, which is defined as "minimal sufficient structure", so as to maintain the accurancy and robustness. How to obtain such structure in a principled way? In this paper, we theoretically prove that if we optimize basic views and final view based on mutual information, and keep their performance on labels simultaneously, the final view will be a minimal sufficient structure. With this guidance, we propose a Compact GSL architecture by MI compression, named CoGSL. Specifically, two basic views are extracted from original graph as two inputs of the model, which are refinedly reestimated by a view estimator. Then, we propose an adaptive technique to fuse estimated views into the final view. Furthermore, we maintain the performance of estimated views and the final view and reduce the mutual information of every two views. To comprehensively evaluate the performance of CoGSL, we conduct extensive experiments on several datasets under clean and attacked conditions, which demonstrate the effectiveness and robustness of CoGSL.
翻译:最近,在优化图形结构以及同时学习图形神经网络(GNNS)的适当参数的能力方面,目前GL方法主要从单一或多个信息来源(基本观点)学习最佳图形结构(最终观点),然而,关于什么是最佳图形结构的理论指导仍未探讨。在本质上,最佳图形结构应仅包含任务信息,同时尽可能压缩多余的噪音,将其定义为“最小足够的结构”,以保持准确性和稳健性。如何以有原则的方式获得这种结构?在本文件中,我们理论上证明,如果我们在相互信息的基础上优化基本观点和最终观点,同时在标签上保持其性能,那么最终观点将是最低限度的足够结构。在这种指导下,我们提出一个以MI压缩(称为CoGSL)为名称的常规GSL结构。具体地说,从原始图表中提取了两种基本观点,作为受攻击的两种投入,并经过一个估测师的精确估计。然后,我们提出一种适应性技术,将精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细地将精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细的精细图。