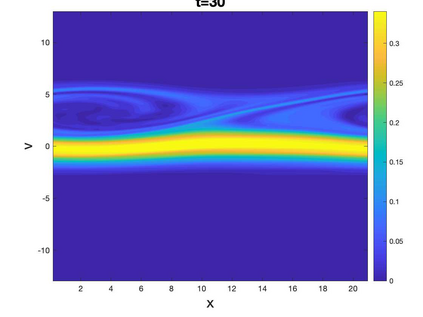
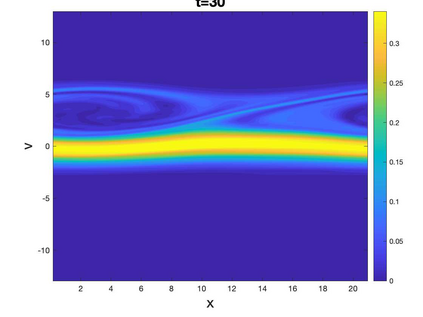
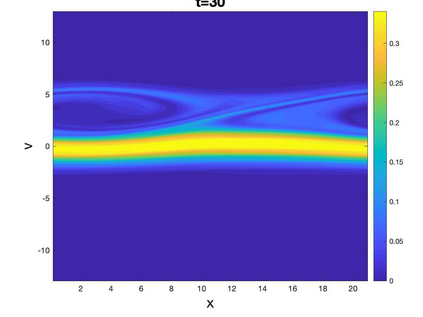
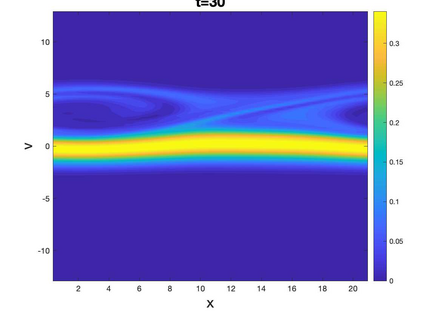
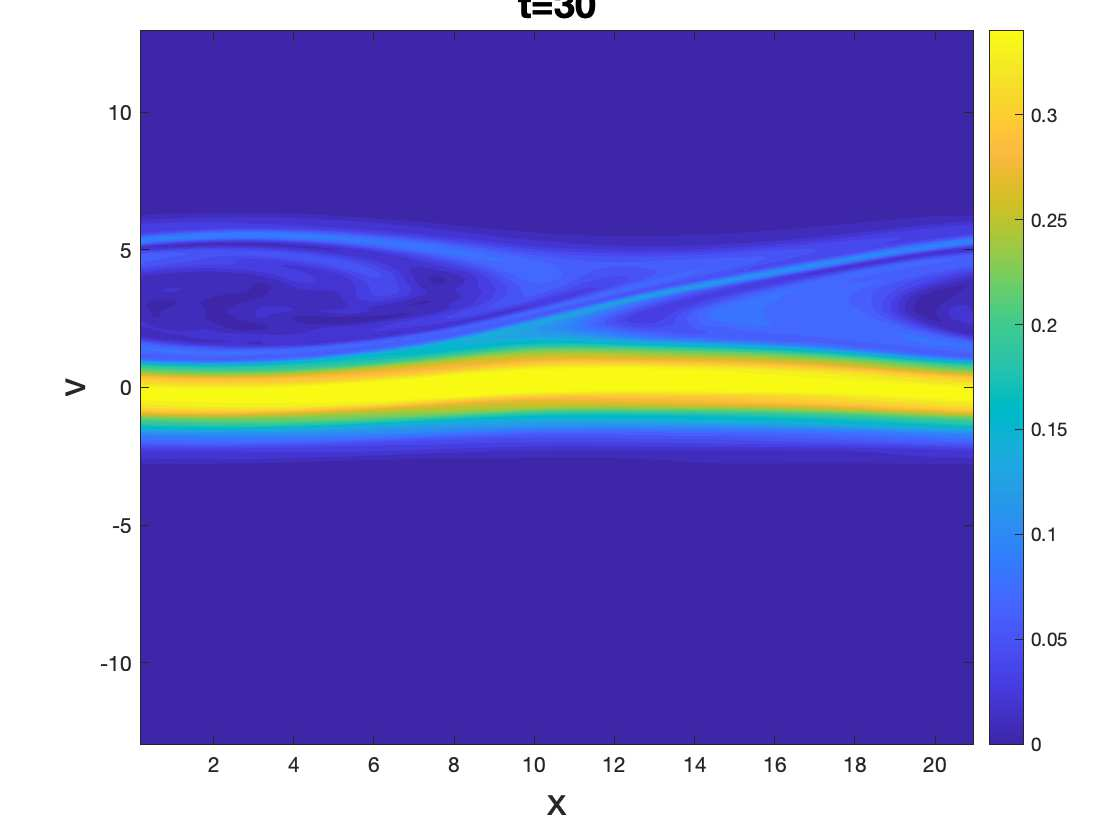
In this paper, we propose a novel Local Macroscopic Conservative (LoMaC) low rank tensor method for simulating the Vlasov-Poisson (VP) system. The LoMaC property refers to the exact local conservation of macroscopic mass, momentum and energy at the discrete level. This is a follow-up work of our previous development of a conservative low rank tensor approach for Vlasov dynamics (arXiv:2201.10397). In that work, we applied a low rank tensor method with a conservative singular value decomposition (SVD) to the high dimensional VP system to mitigate the curse of dimensionality, while maintaining the local conservation of mass and momentum. However, energy conservation is not guaranteed, which is a critical property to avoid unphysical plasma self-heating or cooling. The new ingredient in the LoMaC low rank tensor algorithm is that we simultaneously evolve the macroscopic conservation laws of mass, momentum and energy using a flux-difference form with kinetic flux vector splitting; then the LoMaC property is realized by projecting the low rank kinetic solution onto a subspace that shares the same macroscopic observables by a conservative orthogonal projection. The algorithm is extended to the high dimensional problems by hierarchical Tuck decomposition of solution tensors and a corresponding conservative projection algorithm. Extensive numerical tests on the VP system are showcased for the algorithm's efficacy.
翻译:在本文中, 我们提出了一个新颖的本地宏观保守( LoMaC) 低等级调控( LoMaC) 方法, 用于模拟 Vlasov- Poisson (VP) 系统。 LoMaC 属性指的是在离散级别上对宏观质量、 动力和能量进行精确的本地保护。 这是我们先前为 Vlasov 动态( arXiv: 2201.03. 103.97) 开发的保守的低级别 Exor 方法( LoMaC) 的后续工作。 在这项工作中, 我们用一种保守的单价调控系统( SVD) 低等级调控调( SVD) 来减轻维度的诅咒, 同时维护本地质量和动力。 然而, 能源节制并不是一项至关重要的特性, 以避免非物理等等离子自热或冷。 低等级调算法中的新成分是, 我们同时用一种通量通量矢量矢量矢量分解的通缩( SVMaC 属性) 系统, 通过预测低等级等级的高级递算法, 通过高等级递进度递进度的递化系统, 直压的递进化( VSq) 的递进化( VSR) 递进化( VLAC) 解) 的递进化( VAL) 解) 的递化( VLAC) 解( VAL) 解( VAL) 解( VAL) 解) 解( VAL) 解) 解( VAL) 解) 解决方案在次的 的 的系统上, 通过测( VSRVLVLVLVL) 解( VAL) 解( VALV) 解( VAL) 解( VAL) ) 解( VL) 解( VL) ) 解( VL) 解( VL) 解( VL) 解( VAL) ) 解( VAL) 解( VL) 解( VAL) 的 的 的 ) 解( VAL) ) 解( VAL) 解( VAL) 解) 解) 解) 解( VAL) 的 解( VAL)