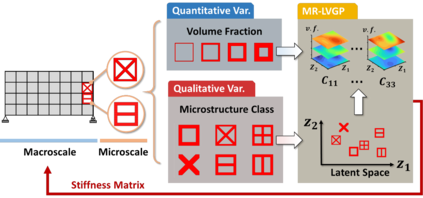
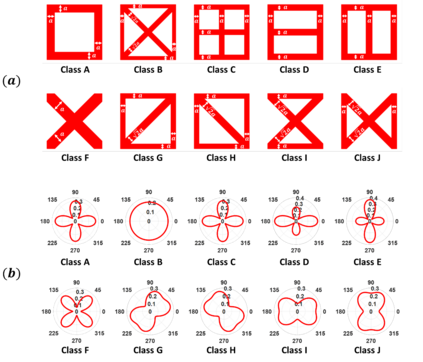
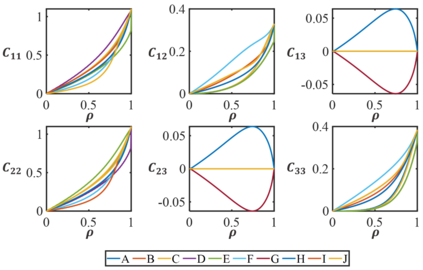
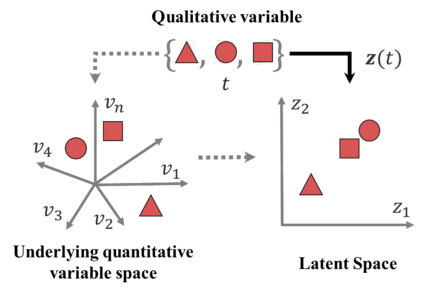
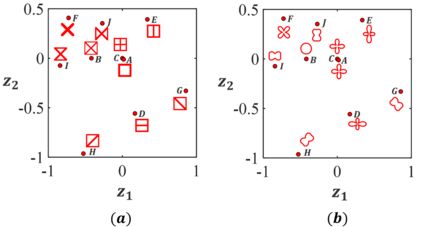
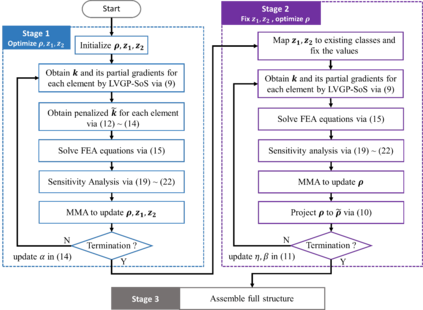
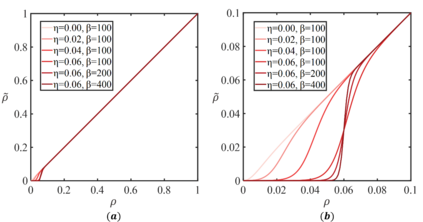
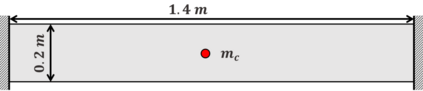
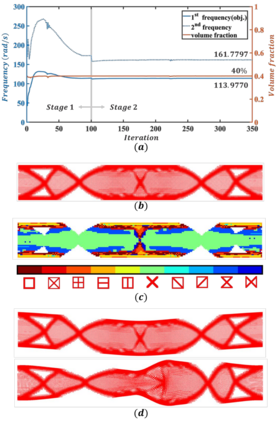
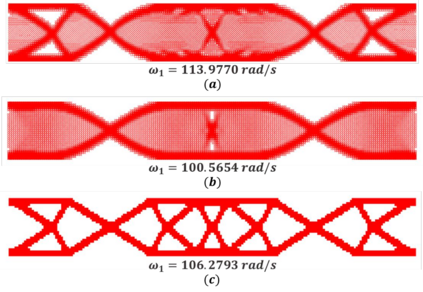
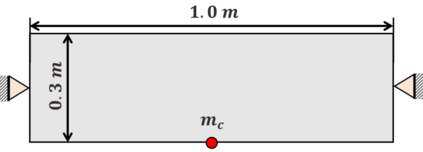
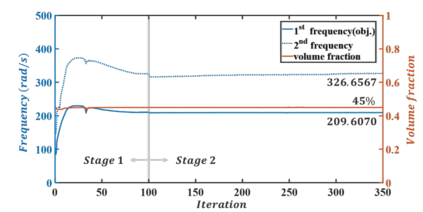
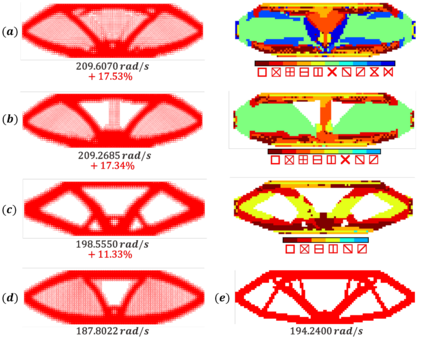
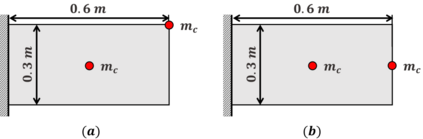
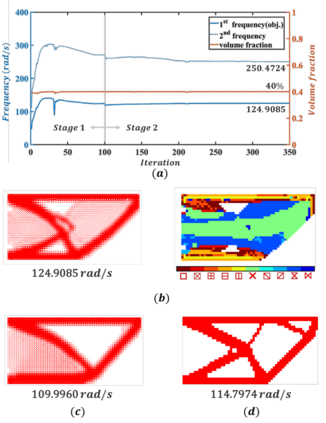
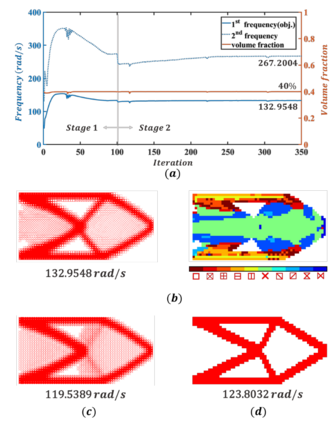
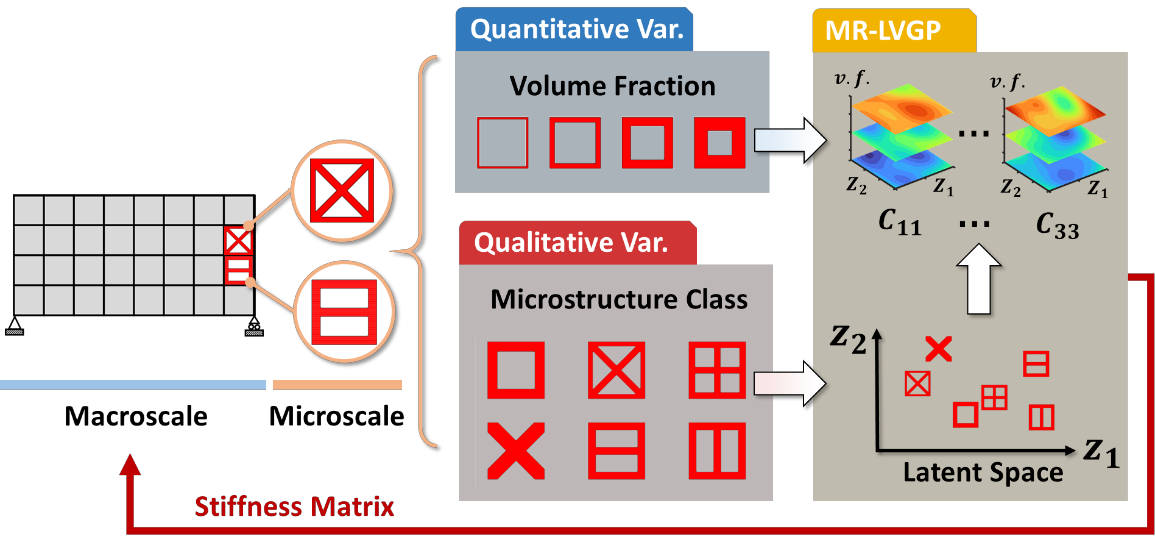
For natural frequency optimization of engineering structures, cellular composites have been shown to possess an edge over solid. However, existing multiscale design methods for cellular composites are either computationally exhaustive or confined to a single class of microstructures. In this paper, we propose a data-driven topology optimization (TO) approach to enable the multiscale design of cellular structures with various choices of microstructure classes. The key component is a newly proposed latent-variable Gaussian process (LVGP) model through which different classes of microstructures are mapped into a low-dimensional continuous latent space. It provides an interpretable distance metric between classes and captures their effects on the homogenized stiffness tensors. By introducing latent vectors as design variables, a differentiable transition of stiffness matrix between classes can be easily achieved with an analytical gradient. After integrating LVGP with the density-based TO, an efficient data-driven cellular composite optimization process is developed to enable concurrent exploration of microstructure concepts and the associated volume fractions for natural frequency optimization. Examples reveal that the proposed cellular designs with multiclass microstructures achieve higher natural frequencies than both single-scale and single-class designs. This framework can be easily extended to other multi-scale TO problems, such as thermal compliance and dynamic response optimization.
翻译:对于工程结构的自然频率优化而言,细胞复合物被证明拥有一个固态的边缘;然而,现有的细胞复合物多尺度设计方法要么在计算上是详尽无遗的,要么局限于单一等级的微结构;在本文件中,我们提议了一种数据驱动的地形优化(TO)办法,以便能够以多种选择的微结构类别来对蜂蜜结构进行多尺度的设计设计;关键组成部分是一个新提议的潜伏可变高萨进程(LVGP)模型,通过这一模型,不同等级的微结构将绘制成一个低维的连续潜伏空间;它提供各等级之间可解释的距离指标,并捕捉到其对同源性僵硬性坚硬度电压的影响;通过采用潜在的矢量器作为设计变量,各等级之间僵硬度矩阵的可轻易地以分析梯度转换;在将LVGP与以密度为基础的各种结构相结合后,将开发一个高效的数据驱动的细胞复合优化过程,以便能够同时探索微结构概念和与自然频率优化相关的体积积分数;例子表明,拟议的多级微结构的细胞结构设计可实现比单级和单级的更高自然频率的自然频率的频率,作为多级的响应。这个框架可以容易扩大至其他的周期性、制成。