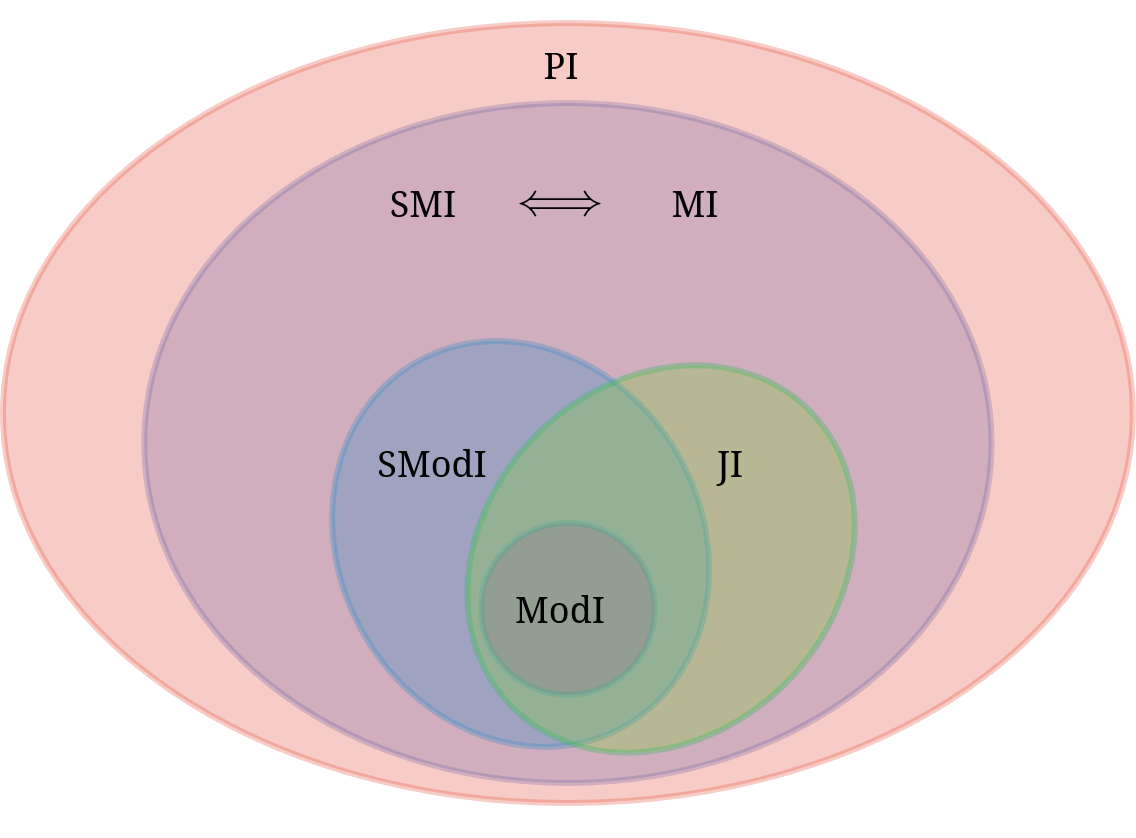
Recently a class of generalized information measures was defined on sets of items parametrized by submodular functions. In this paper, we propose and study various notions of independence between sets with respect to such information measures, and connections thereof. Since entropy can also be used to parametrize such measures, we derive interesting independence properties for the entropy of sets of random variables. We also study the notion of multi-set independence and its properties. Finally, we present optimization algorithms for obtaining a set that is independent of another given set, and also discuss the implications and applications of combinatorial independence.
翻译:最近,根据子模块功能,对各组物品界定了一类通用信息措施。在本文中,我们提出并研究各组之间在这类信息措施及其连接方面的各种独立概念。由于可使用英特罗比来对此类措施进行对称,我们为各组随机变量的英特罗比获取有趣的独立特性。我们还研究多组独立概念及其属性。最后,我们提出优化算法,以获得一组独立于另一组的商品,并讨论组合独立的影响和应用。