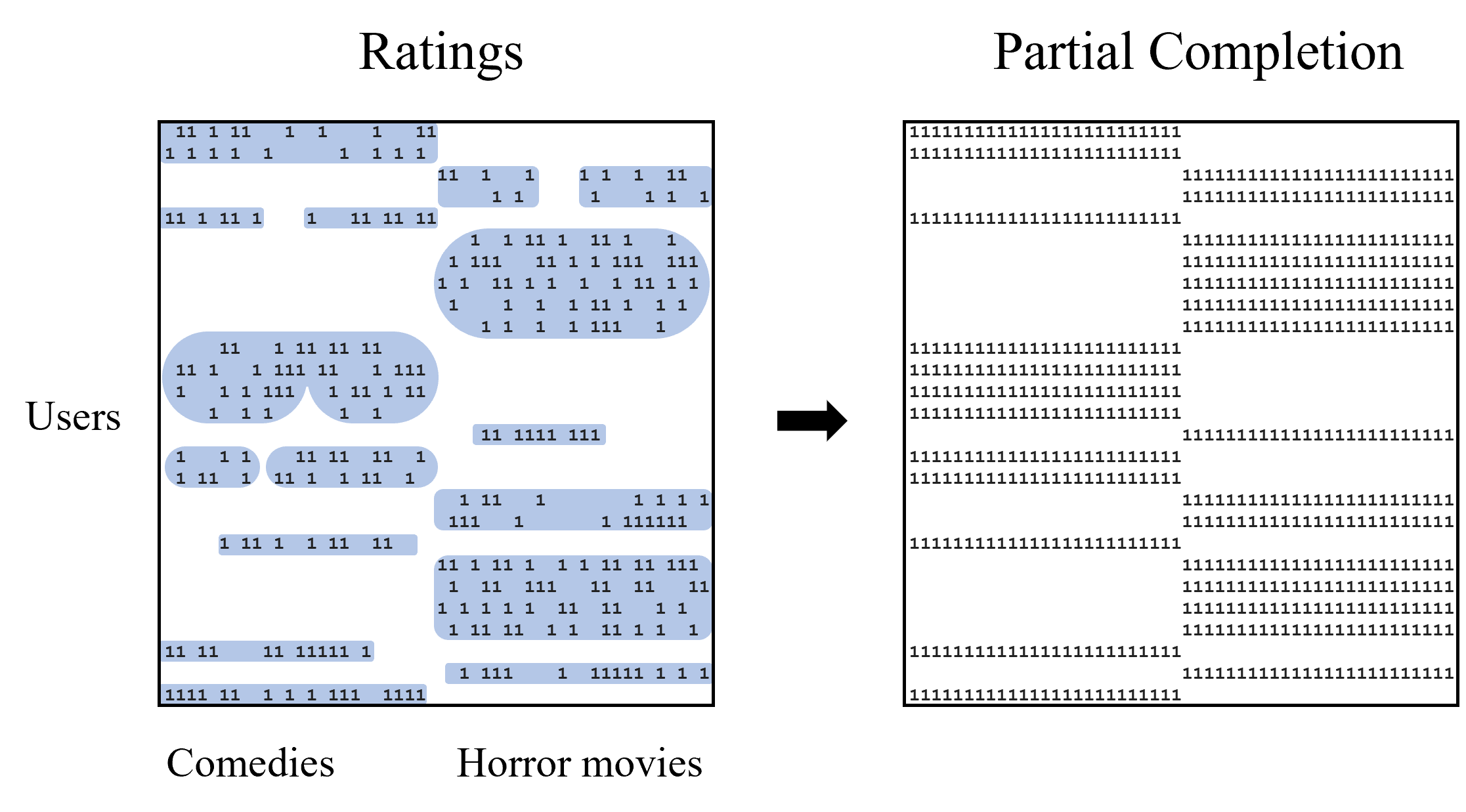
In the matrix completion problem, one wishes to reconstruct a low-rank matrix based on a revealed set of (possibly noisy) entries. Prior work considers completing the entire matrix, which may be highly inaccurate in the common case where the distribution over entries is non-uniform. We formalize the problem of Partial Matrix Completion where the goal is to complete a large subset of the entries, or equivalently to complete the entire matrix and specify an accurate subset of the entries. Interestingly, even though the distribution is unknown and arbitrarily complex, our efficient algorithm is able to guarantee: (a) high accuracy over all completed entries, and (b) high coverage, meaning that it covers at least as much of the matrix as the distribution of observations.
翻译:在矩阵完成问题中,人们希望根据一套公开的(可能吵闹的)条目重建一个低级矩阵; 以往的工作考虑完成整个矩阵,在对条目的分布不统一的常见情况下,这可能非常不准确; 我们正式确定部分矩阵完成问题,目标是完成一大部分条目,或相当于完成整个矩阵,并指定一个准确的条目子。 有趣的是,尽管分布不为人所知,而且任意复杂,但我们高效的算法能够保证:(a) 对所有已完成条目的准确性很高,以及(b) 涵盖面大,这意味着它至少涵盖矩阵中的一大部分,与观察的分布一样。