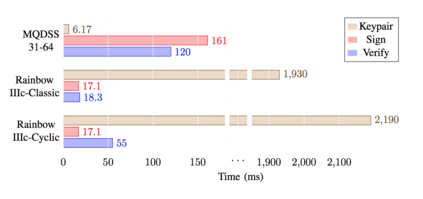
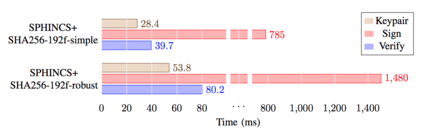
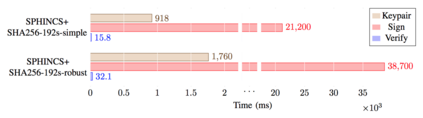
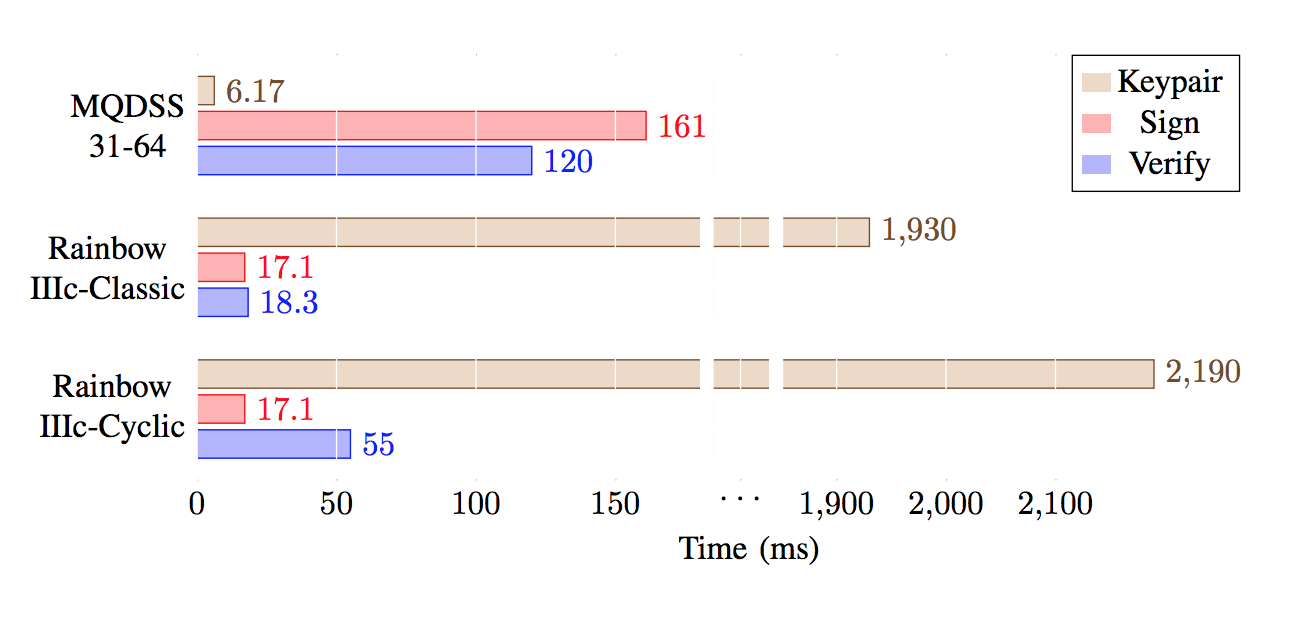
Advances in quantum computing make Shor's algorithm for factorising numbers ever more tractable. This threatens the security of any cryptographic system which often relies on the difficulty of factorisation. It also threatens methods based on discrete logarithms, such as with the Diffie-Hellman key exchange method. For a cryptographic system to remain secure against a quantum adversary, we need to build methods based on a hard mathematical problem, which are not susceptible to Shor's algorithm and which create Post Quantum Cryptography (PQC). While high-powered computing devices may be able to run these new methods, we need to investigate how well these methods run on limited powered devices. This paper outlines an evaluation framework for PQC within constrained devices, and contributes to the area by providing benchmarks of the front-running algorithms on a popular single-board low-power device.
翻译:量子计算的进步使得Shor的数值乘数算法更加容易移动。 这威胁到常常依赖因数化难度的任何加密系统的安全。 它还威胁到基于离散对数的方法,例如Diffie-Hellman键交换法。 为使加密系统对量子对子交换法保持安全,我们需要根据一个硬数学问题来建立方法,这些方法不易受到Shor算法的影响,并且创造了Qantum后加密(PQC ) 。 虽然高功率的计算机设备可能能够运行这些新方法,但我们需要调查这些方法在有限的动力装置上运行的好坏。 本文概述了在限制装置内对PQC的评估框架,并通过在流行的单板低功率装置上提供前行算法的基准,为该地区做出贡献。