Microbiome subcommunity learning with logistic-tree normal latent Dirichlet allocation

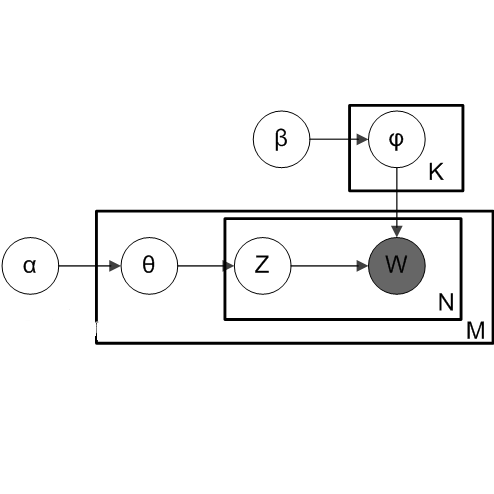
Mixed-membership (MM) models such as Latent Dirichlet Allocation (LDA) have been applied to microbiome compositional data to identify latent subcommunities of microbial species. However, microbiome compositional data, especially those collected from the gut, typically display substantial cross-sample heterogeneities in the subcommunity composition which current MM methods do not account for. To address this limitation, we incorporate the logistic-tree normal (LTN) model -- using the phylogenetic tree structure -- into the LDA model to form a new MM model. This model allows variation in the composition of each subcommunity around some ``centroid'' composition. Incorporation of auxiliary P\'olya-Gamma variables enables a computationally efficient collapsed blocked Gibbs sampler to carry out Bayesian inference under this model. We compare the new model and LDA and show that in the presence of large cross-sample heterogeneity, under the LDA model the resulting inference can be extremely sensitive to the specification of the total number of subcommunities as it does not account for cross-sample heterogeneity. As such, the popular strategy in other applications of MM models of overspecifying the number of subcommunities -- and hoping that some meaningful subcommunities will emerge among artificial ones -- can lead to highly misleading conclusions in the microbiome context. In contrast, by accounting for such heterogeneity, our MM model restores the robustness of the inference in the specification of the number of subcommunities and again allows meaningful subcommunities to be identified under this strategy.