Nonparametric Bayesian volatility estimation for gamma-driven stochastic differential equations

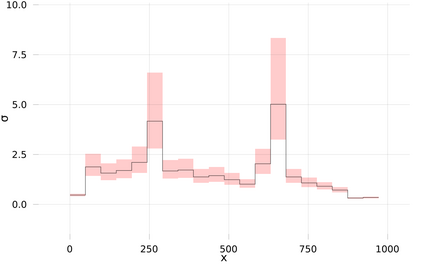
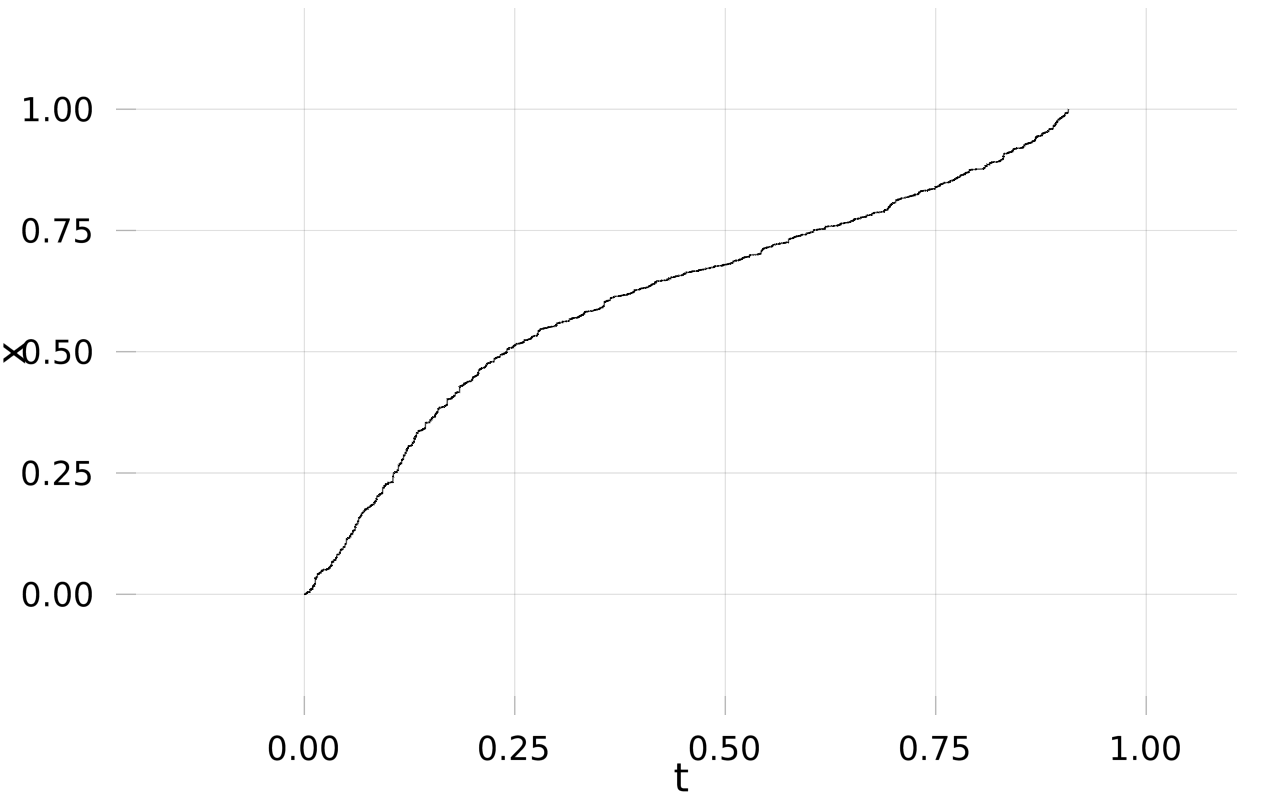
We study a nonparametric Bayesian approach to estimation of the volatility function of a stochastic differential equation driven by a gamma process. The volatility function is modelled a priori as piecewise constant, and we specify a gamma prior on its values. This leads to a straightforward procedure for posterior inference via an MCMC procedure. We give theoretical performance guarantees (contraction rates for the posterior) for the Bayesian estimate in terms of the regularity of the unknown volatility function. We illustrate the method on synthetic and real data examples.