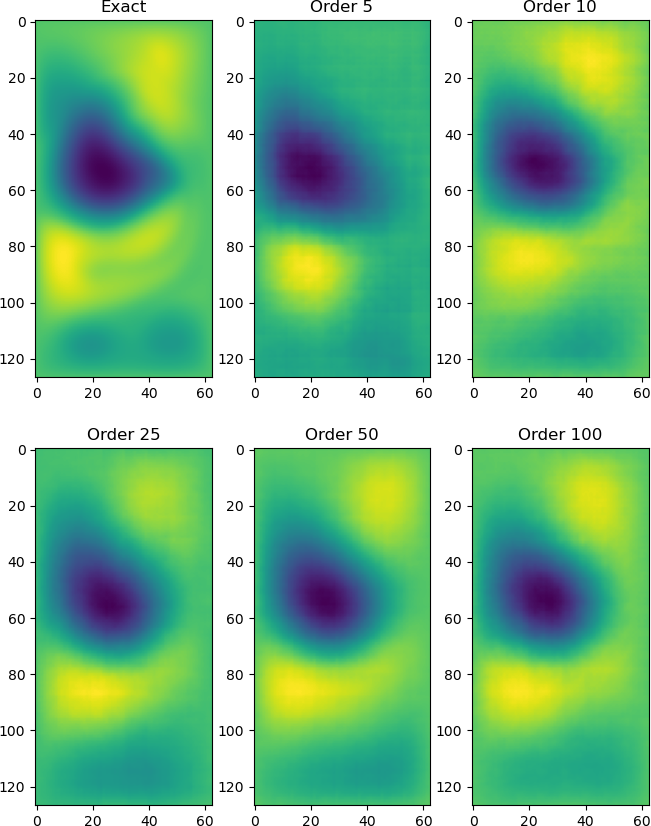
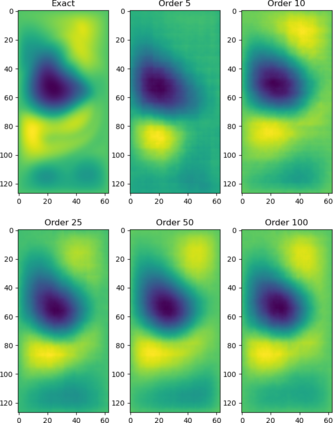
Reduced order modeling (ROM) is a field of techniques that approximates complex physics-based models of real-world processes by inexpensive surrogates that capture important dynamical characteristics with a smaller number of degrees of freedom. Traditional ROM techniques such as proper orthogonal decomposition (POD) focus on linear projections of the dynamics onto a set of spectral features. In this paper we explore the construction of ROM using autoencoders (AE) that perform nonlinear projections of the system dynamics onto a low dimensional manifold learned from data. The approach uses convolutional neural networks (CNN) to learn spatial features as opposed to spectral, and utilize a physics informed (PI) cost function in order to capture temporal features as well. Our investigation using the quasi-geostrophic equations reveals that while the PI cost function helps with spatial reconstruction, spatial features are less powerful than spectral features, and that construction of ROMs through machine learning-based methods requires significant investigation into novel non-standard methodologies.
翻译:降序建模(ROM)是一个技术领域,它通过廉价的代孕技术,将基于物理的复杂真实世界过程模型与基于物理的复杂模型相近,这种代孕能捕捉到重要的动态特征,自由度较低; 传统的ROM技术,例如适当的正正正分分解(POD),侧重于对一系列光谱特征的动态线性预测; 本文中我们探讨利用对系统动态进行非线性预测的自动解析器(AE),将系统动态进行非线性预测,转化为从数据中学习的低维元元元; 这种方法利用革命神经网络(CNN)学习空间特征而不是光谱,并利用物理学知情(PI)成本功能,以捕捉时间特征。 我们使用准地球营养方程式进行的调查显示,虽然PI的成本功能有助于空间重建,但空间特征比光谱特征的强度要小,通过机器学习方法建造ROM需要大量调查新的非标准方法。