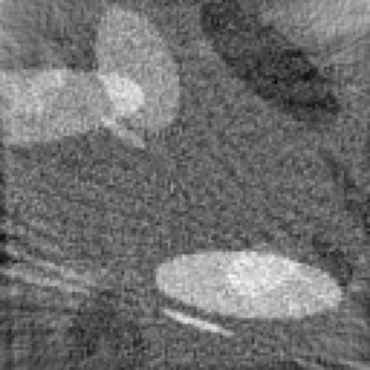
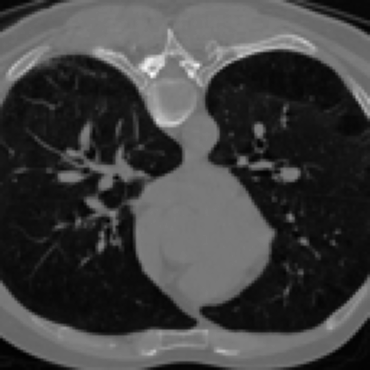
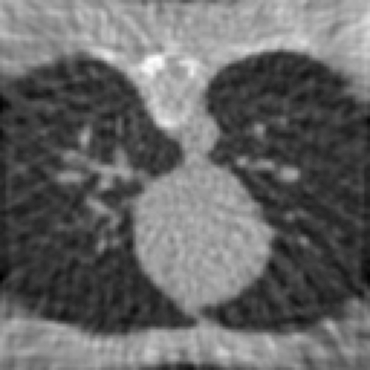
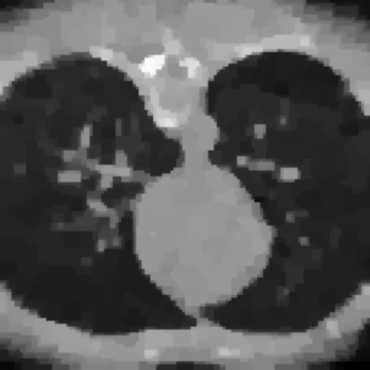
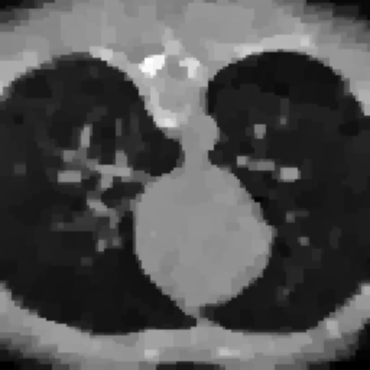
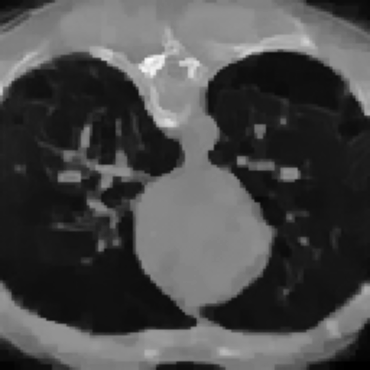
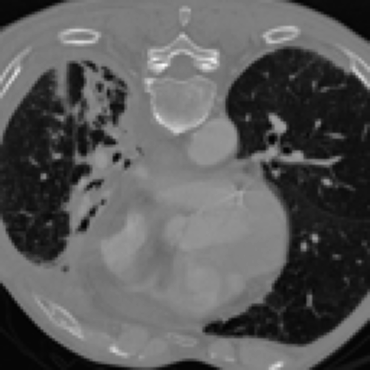
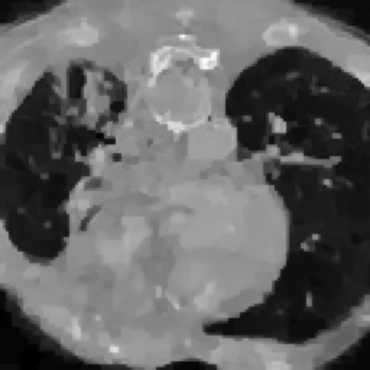
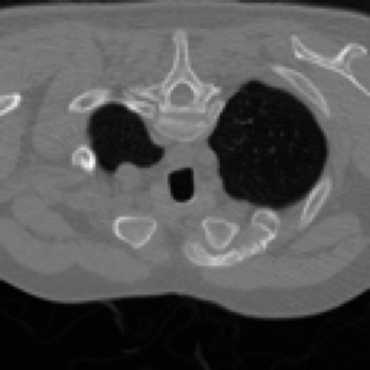
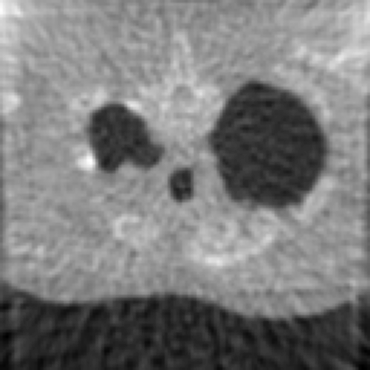
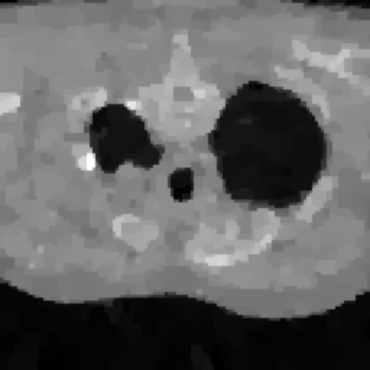
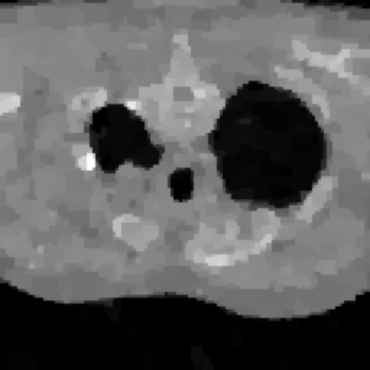
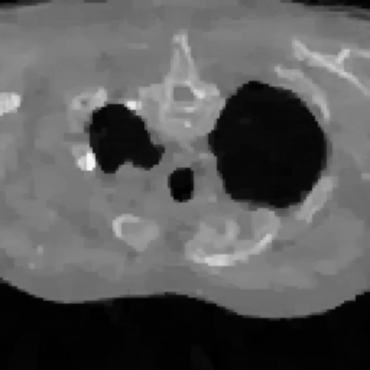
Inverse problems consist of recovering a signal from a collection of noisy measurements. These are typically cast as optimization problems, with classic approaches using a data fidelity term and an analytic regularizer that stabilizes recovery. Recent Plug-and-Play (PnP) works propose replacing the operator for analytic regularization in optimization methods by a data-driven denoiser. These schemes obtain state of the art results, but at the cost of limited theoretical guarantees. To bridge this gap, we present a new algorithm that takes samples from the manifold of true data as input and outputs an approximation of the projection operator onto this manifold. Under standard assumptions, we prove this algorithm generates a learned operator, called Wasserstein-based projection (WP), that approximates the true projection with high probability. Thus, WPs can be inserted into optimization methods in the same manner as PnP, but now with theoretical guarantees. Provided numerical examples show WPs obtain state of the art results for unsupervised PnP signal recovery.
翻译:反面的问题包括从一群吵闹的测量中恢复信号。 这些问题通常被描绘成优化问题, 典型的方法是使用数据忠诚术语和稳定恢复的分析性常规化器。 最近的插件和布料( PnP) 工程建议用数据驱动的代名词取代操作者在优化方法中进行分析性规范化。 这些计划取得了最新的结果, 但以有限的理论保障为代价。 为了缩小这一差距, 我们提出了一个新的算法, 从多种真实数据中提取样本作为输入和输出的样本, 将投影操作员近似于此多元数据。 根据标准假设, 我们证明这种算法产生了一个学习的操作者, 叫做瓦塞斯坦的投影( WP ), 其近似于真实预测的概率很高 。 因此, WP 可以用与 PnP 相同的方式插入优化方法, 但现在有理论保障。 提供的数字示例显示, WP 获得未被超过的 PnP 信号恢复的艺术结果状态 。