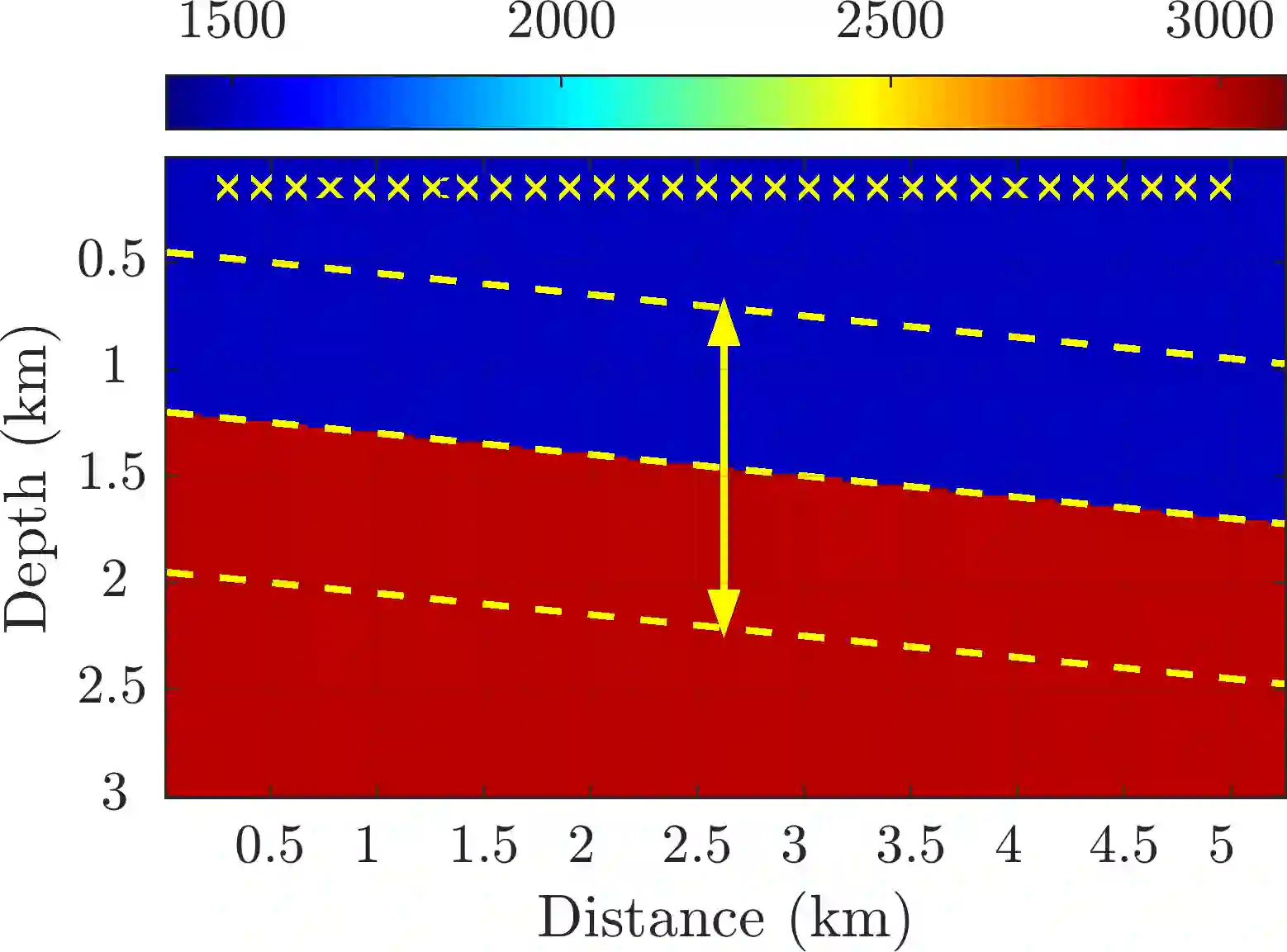
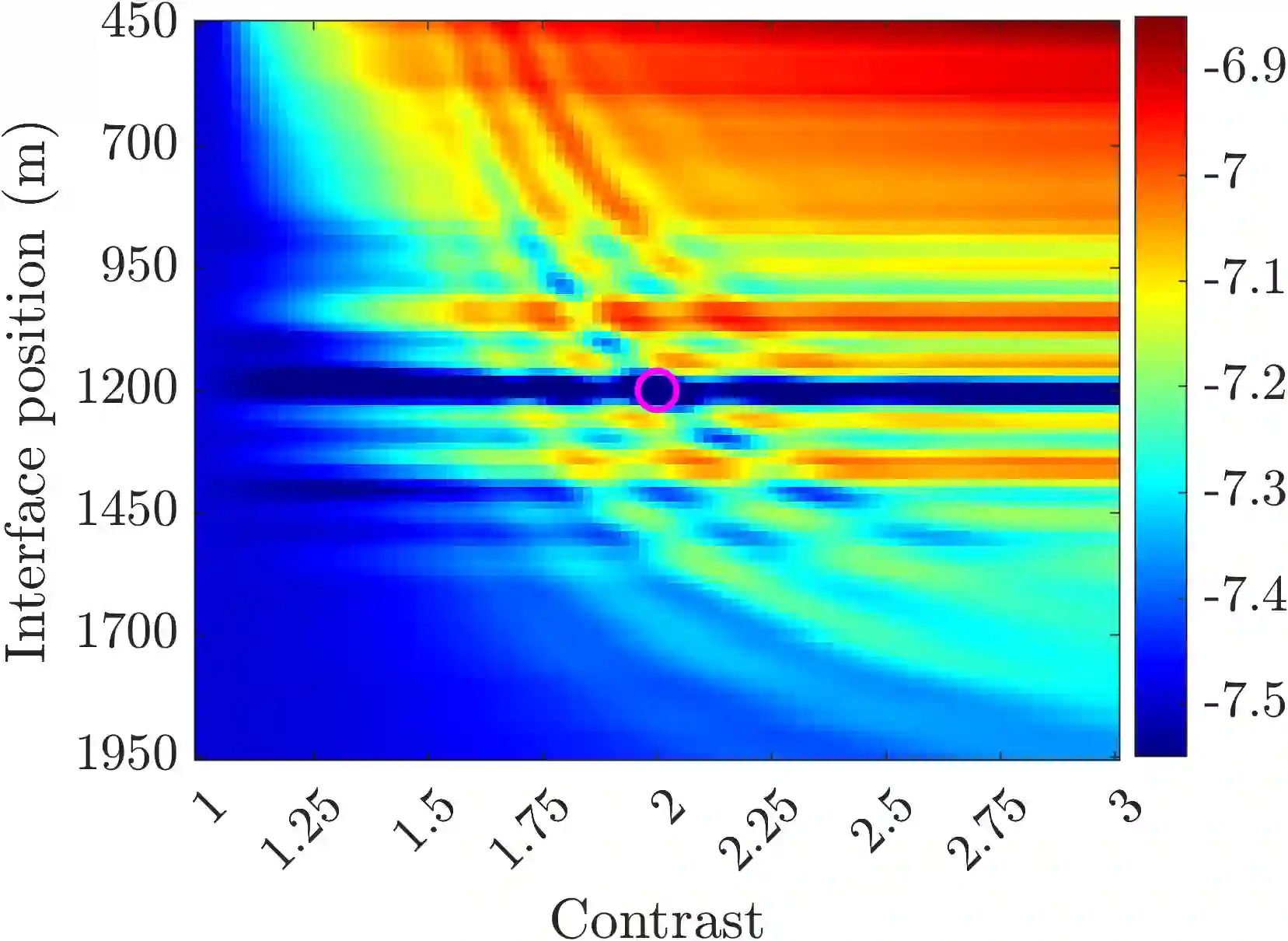
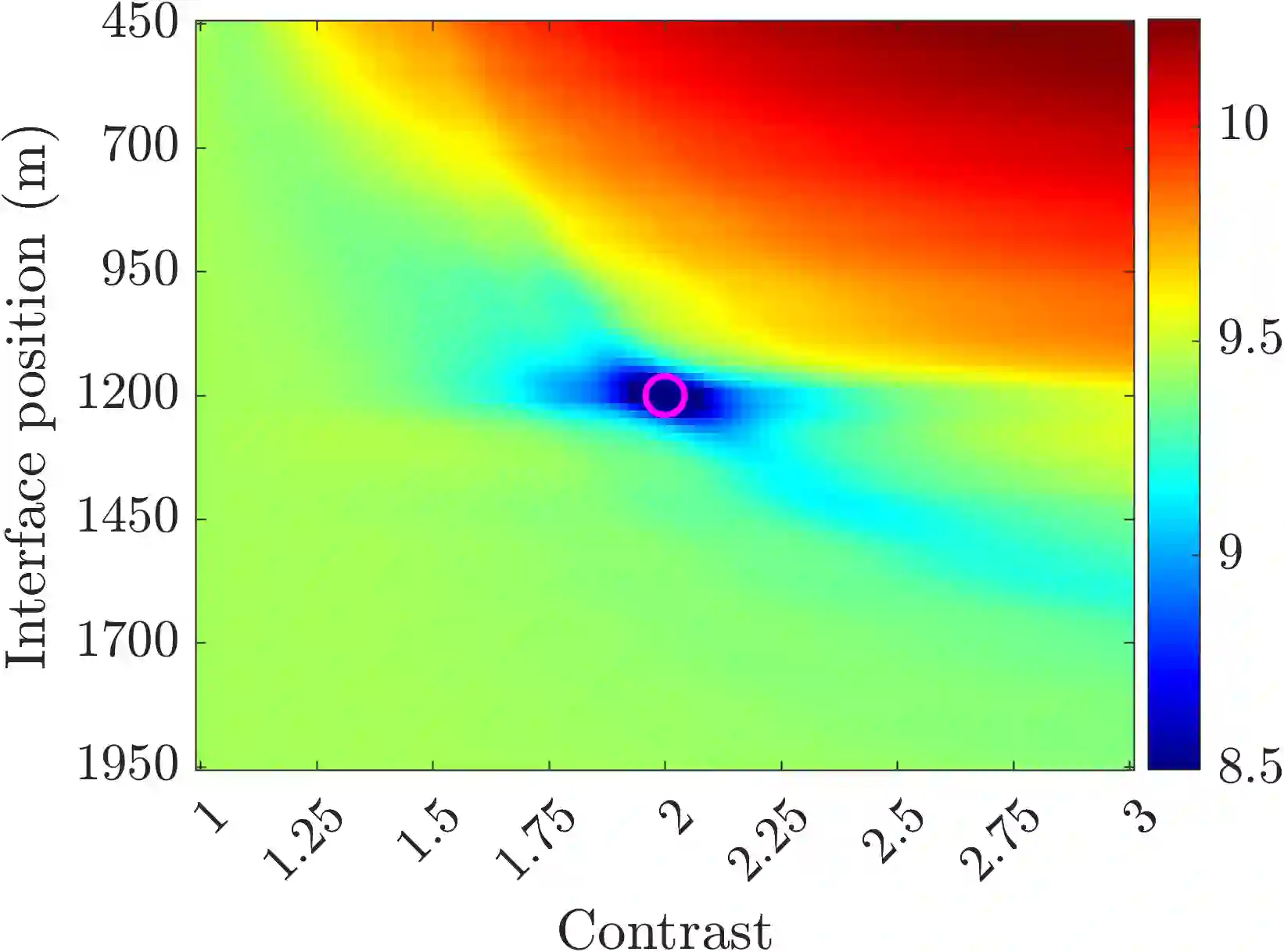
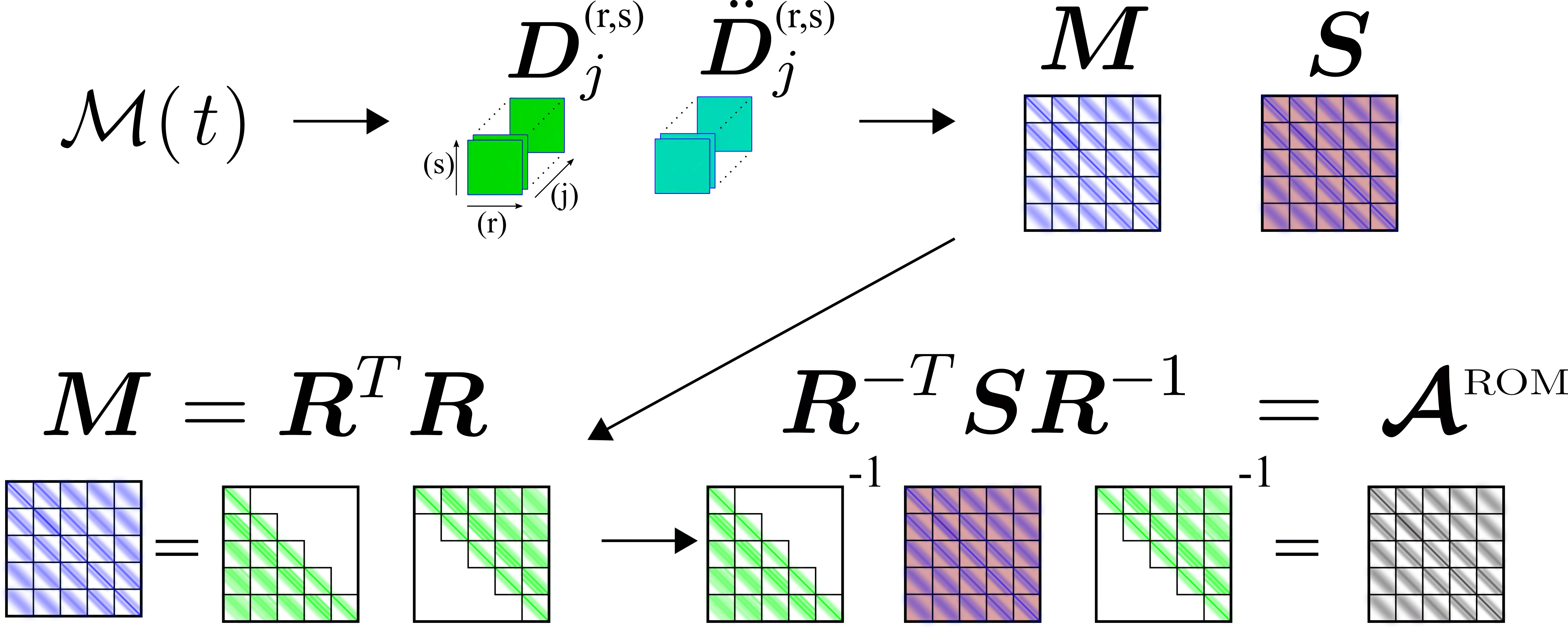We introduce a novel approach to waveform inversion, based on a data driven reduced order model (ROM) of the wave operator. The presentation is for the acoustic wave equation, but the approach can be extended to elastic or electromagnetic waves. The data are time resolved measurements of the pressure wave gathered by an acquisition system which probes the unknown medium with pulses and measures the generated waves. We propose to solve the inverse problem of velocity estimation by minimizing the square misfit between the ROM computed from the recorded data and the ROM computed from the modeled data, at the current guess of the velocity. We give the step by step computation of the ROM, which depends nonlinearly on the data and yet can be obtained from them in a non-iterative fashion, using efficient methods from linear algebra. We also explain how to make the ROM robust to data inaccuracy. The ROM computation requires the full array response matrix gathered with collocated sources and receivers. However, we show that the computation can deal with an approximation of this matrix, obtained from towed-streamer data using interpolation and reciprocity on-the-fly. While the full-waveform inversion approach of nonlinear least-squares data fitting is challenging without low frequency information, due to multiple minima of the data fit objective function, we show that the ROM misfit objective function has a better behavior, even for a poor initial guess. We also show by an explicit computation of the objective functions in a simple setting that the ROM misfit objective function has convexity properties, whereas the least squares data fit objective function displays multiple local minima.
翻译:我们引入了一种新颖的波形倒置方法, 其依据是数据驱动的降低波控操作员的调序模型( ROM) 。 演示是用于声波方程式的, 但该方法可以扩展至弹性波或电磁波。 数据是用于探测未知介质和测量生成波的获取系统所收集的压力波的时间溶解度。 我们提议通过将记录的数据和模型数据计算出来的ROM之间的方位错配最小化来解决速度估算的反向问题。 我们用当前速度的猜测, 我们用声波波方程式逐步计算, 但它可以不线性能或电磁波。 数据是用直线变数系统收集的高效方法对压力波进行时间解析测量, 我们还解释了如何使ROM与数据不准确性。 ROM计算需要用相交替的源和接收器收集的全阵列响应矩阵。 然而, 我们表明, 计算可以处理这个从最差的流数据基流数据中获取到最差的基流数据, 以非线不直线和对等的对等方式以非直径直径直径的方式从数据函数 。, 显示一个不直径的轨道的极的轨道显示的轨道运行功能, 显示一个不直径直径直径直径的轨道, 。 显示一个不直径直径直径直径直径直径的轨道运行的轨道运行的轨道运行的轨道功能。