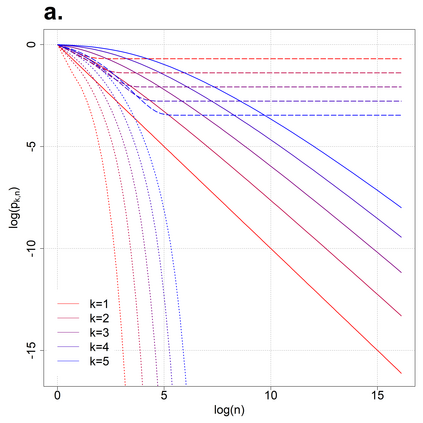
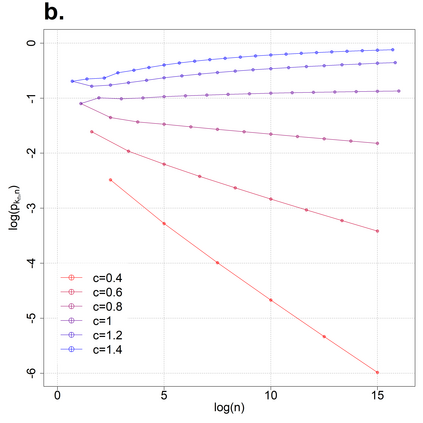
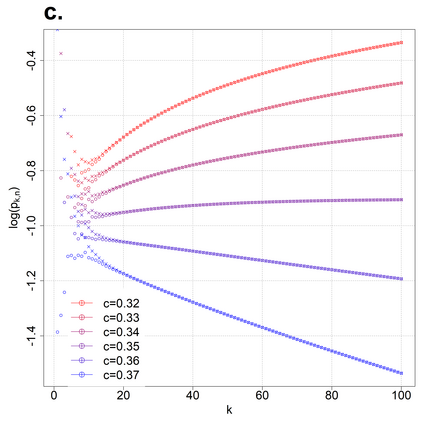
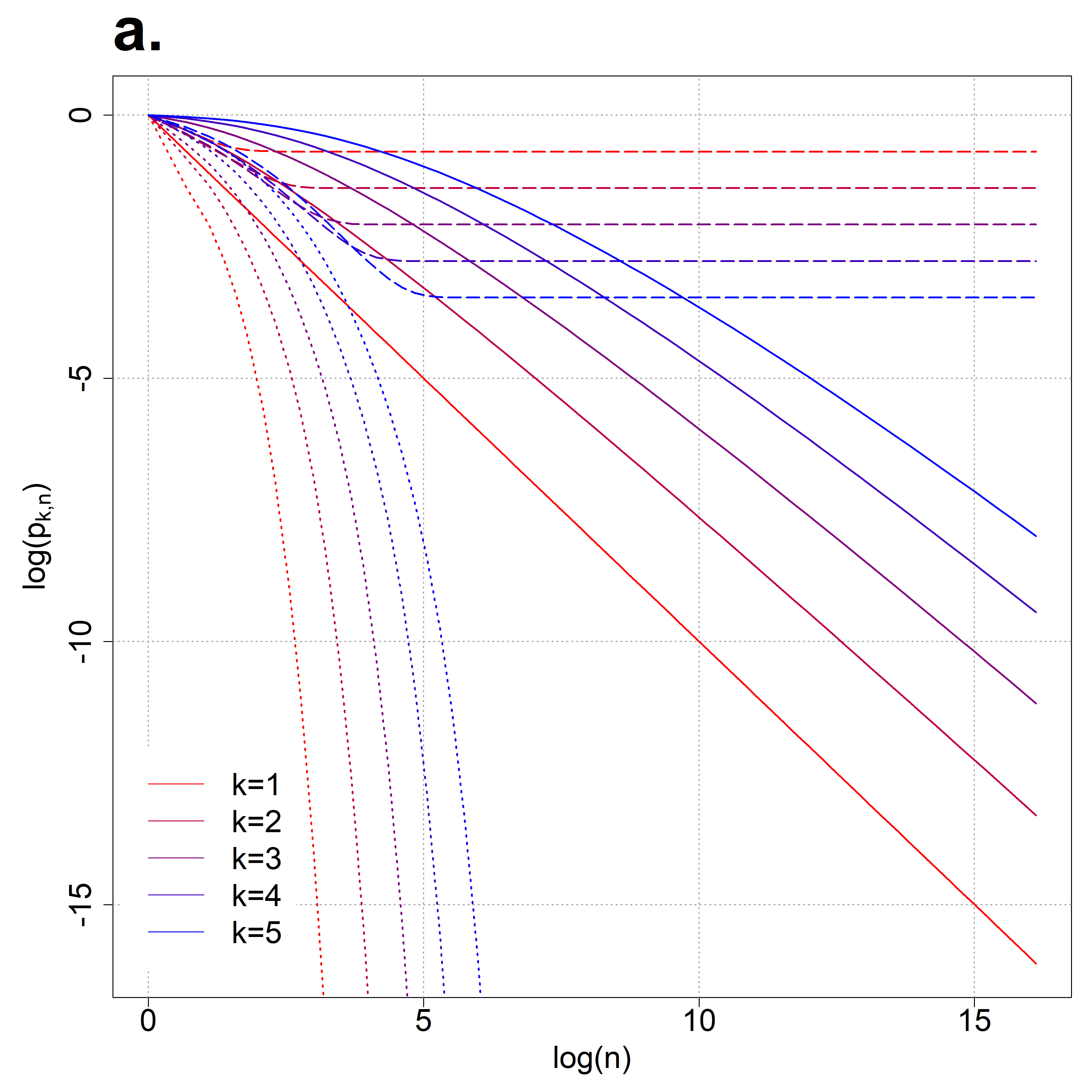
Consider $n$ iid real-valued random vectors of size $k$ having iid coordinates with a general distribution function $F$. A vector is a maximum if and only if there is no other vector in the sample which weakly dominates it in all coordinates. Let $p_{k,n}$ be the probability that the first vector is a maximum. The main result of the present paper is that if $k\equiv k_n$ is growing at a slower (faster) rate than a certain factor of $\log(n)$, then $p_{k,n} \rightarrow 0$ (resp. $p_{k,n}\rightarrow1$) as $n\to\infty$. Furthermore, the factor is fully characterized as a functional of $F$. We also study the effect of $F$ on $p_{k,n}$, showing that while $p_{k,n}$ may be highly affected by the choice of $F$, the phase transition is the same for all distribution functions up to a constant factor.
翻译:考虑美元实际价值为美元的实际随机矢量, 其大小为 $k$, 其坐标为 $(n) 。 矢量是最大值的, 如果并且只有在样本中没有其他矢量在所有坐标中微弱支配该矢量。 让 $p ⁇ k, n} 美元成为第一个矢量最大的可能性。 本文的主要结果是, 如果 $k\ equiv k_n 以较慢( 较快) 的速度增长, 而不是 $( log) 的某个系数, 美元, 然后 $p ⁇ k, n} rightrow $ 0 ( resp. $p ⁇ k, n rightrow1$), 则以 $n\\ t\ t\ t\ inty$为最大值。 此外, 该系数被完全定性为 $( $) 。 我们还研究美元对 $p ⁇ k, n} 美元的影响, 表明 美元可能因选择 $(n) 而受到极大影响,,, 而所有分配功能的阶段过渡与 向一个恒值相同 。