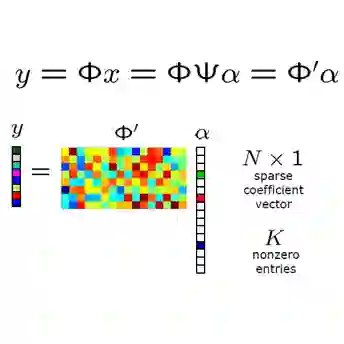
In this paper, we propose a method to predict the asymptotic performance of the alternating direction method of multipliers (ADMM) for compressed sensing, where we reconstruct an unknown structured signal from its underdetermined linear measurements. The derivation of the proposed method is based on the recently developed convex Gaussian min-max theorem (CGMT), which can be applied to various convex optimization problems to obtain its asymptotic error performance. Our main idea is to analyze the convex subproblem in the update of ADMM iteratively and characterize the asymptotic distribution of the tentative estimate obtained at each iteration. However, since the original CGMT cannot be used directly for the analysis of the iterative updates, we intuitively assume an extended version of CGMT in the derivation of the proposed method. Under the assumption, the result shows that the update equations in ADMM can be decoupled into a scalar-valued stochastic process in the asymptotic regime with the large system limit. From the asymptotic result, we can predict the evolution of the error (e.g., mean-square-error (MSE) and symbol error rate (SER)) in ADMM for large-scale compressed sensing problems. Simulation results show that the empirical performance of ADMM and its prediction are close to each other in sparse vector reconstruction and binary vector reconstruction.
翻译:在本文中,我们提出一种方法来预测用于压缩遥感的乘数交替方向方法(ADMM)的无症状性性能,我们从中重建一个由不确定的线性测量得出的未知结构信号。拟议方法的衍生依据是最近开发的 convex Gausian min-max-max 理论(CGMT),该理论可以应用于各种 convex优化问题,以获得其无症状错误性能。我们的主要想法是分析ADMMM更新时迭接地分析的交替方向分问题,并描述每次迭代得出的暂定估计数的无症状性分布。然而,由于最初的CGMT不能直接用于迭代更新分析,我们直觉地假设在拟议方法的衍生过程中,CGMT的扩展版本可以适用于各种对等方,以获得其无症状性能性能的性能。根据大系统限制,分析ADMMMM的降量的硬性能分数过程。从近似性能结果到SIMMS-imalimalimalimalimal immoal orisal immodemodigration maisal dismode,我们可以预测其大性能-ad 。