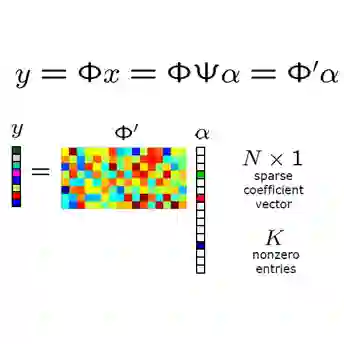
In CS literature, the efforts can be divided into two groups: finding a measurement matrix that preserves the compressed information at the maximum level, and finding a reconstruction algorithm for the compressed information. In the traditional CS setup, the measurement matrices are selected as random matrices, and optimization-based iterative solutions are used to recover the signals. However, when we handle large signals, using random matrices become cumbersome especially when it comes to iterative optimization-based solutions. Even though recent deep learning-based solutions boost the reconstruction accuracy performance while speeding up the recovery, still jointly learning the whole measurement matrix is a difficult process. In this work, we introduce a separable multi-linear learning of the CS matrix by representing it as the summation of arbitrary number of tensors. For a special case where the CS operation is set as a single tensor multiplication, the model is reduced to the learning-based separable CS; while a dense CS matrix can be approximated and learned as the summation of multiple tensors. Both cases can be used in CS of two or multi-dimensional signals e.g., images, multi-spectral images, videos, etc. Structural CS matrices can also be easily approximated and learned in our multi-linear separable learning setup with structural tensor sum representation. Hence, our learnable generalized tensor summation CS operation encapsulates most CS setups including separable CS, non-separable CS (traditional vector-matrix multiplication), structural CS, and CS of the multi-dimensional signals. For both gray-scale and RGB images, the proposed scheme surpasses most state-of-the-art solutions, especially in lower measurement rates. Although the performance gain remains limited from tensor to the sum of tensor representation for gray-scale images, it becomes significant in the RGB case.
翻译:在 CS 文献中, 这项工作可以分为两类: 找到一个在最大水平上保存压缩信息的测量矩阵, 并找到压缩信息的重建算法。 在传统的 CS 设置中, 测量矩阵被选为随机矩阵, 并且使用基于优化的迭代解决方案来恢复信号。 但是, 当我们处理大信号时, 使用随机矩阵变得很麻烦, 特别是当它涉及到迭代优化解决方案时。 尽管最近深层次的基于学习的解决方案在加速恢复的同时提高了重建准确性, 但仍然共同学习整个测量矩阵是一个困难的过程。 在这项工作中, 我们引入了 CS 矩阵的可分解多线性学习。 对于 CS 操作作为任意数的相加。 对于一个特殊案例, 当 CS 操作被设置为单一的变异倍增时, 该模型被降为基于学习的相异性 CS ; 而一个密集的 CS 矩阵则被近于多个变异性阵列, 用于两个或多维信号的 CS, 例如, 图像、 多光谱S 结构图像、 最易的 Csalalal 和 Csloveal 。