A Relaxed Localized Trust-Region Reduced Basis Approach for Optimization of Multiscale Problems

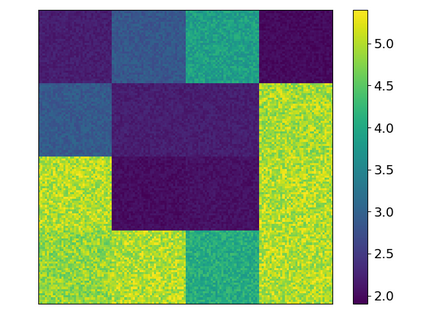
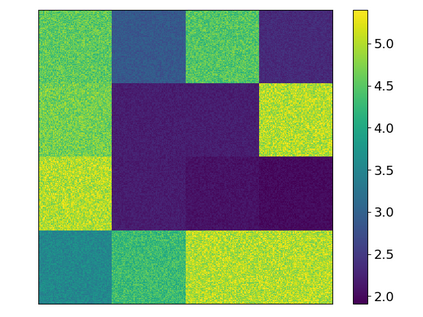
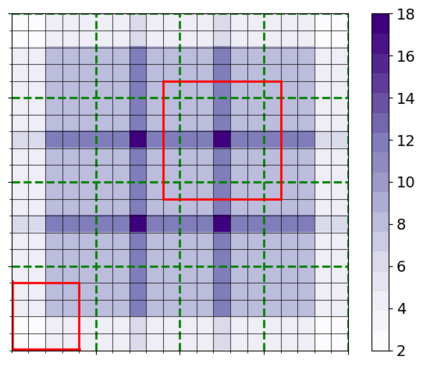
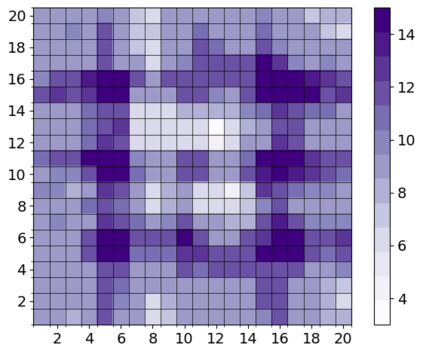
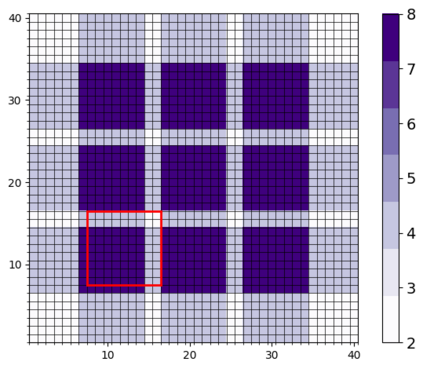
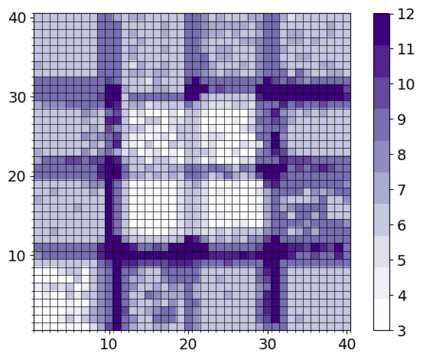
In this contribution, we are concerned with parameter optimization problems that are constrained by multiscale PDE state equations. As an efficient numerical solution approach for such problems, we introduce and analyze a new relaxed and localized trust-region reduced basis method. Localization is obtained based on a Petrov-Galerkin localized orthogonal decomposition method and its recently introduced two-scale reduced basis approximation. We derive efficient localizable a posteriori error estimates for the optimality system, as well as for the two-scale reduced objective functional. While the relaxation of the outer trust-region optimization loop still allows for a rigorous convergence result, the resulting method converges much faster due to larger step sizes in the initial phase of the iterative algorithms. The resulting algorithm is parallelized in order to take advantage of the localization. Numerical experiments are given for a multiscale thermal block benchmark problem. The experiments demonstrate the efficiency of the approach, particularly for large scale problems, where methods based on traditional finite element approximation schemes are prohibitive or fail entirely.