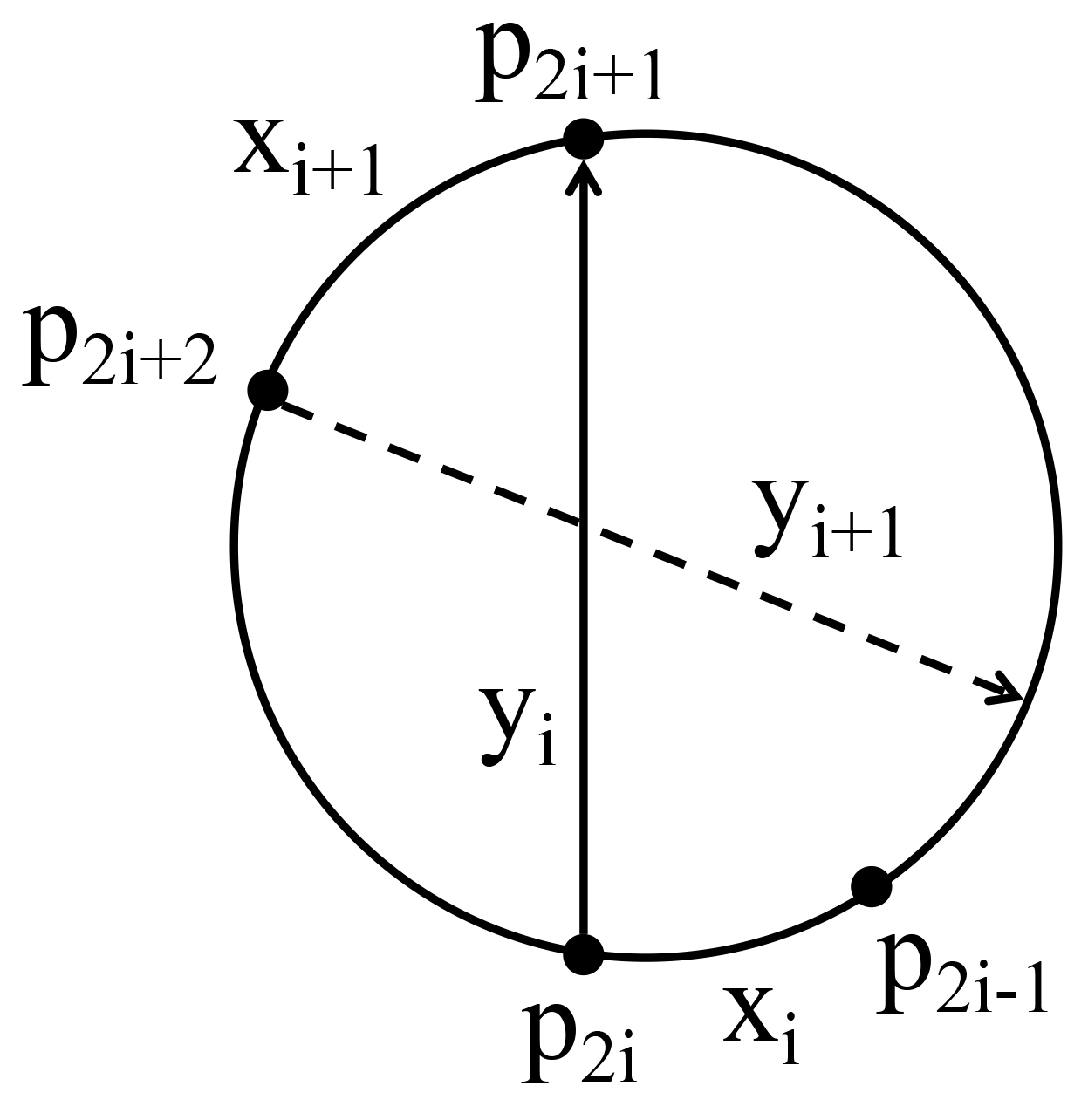
TSP is a classical NP-hard combinatorial optimization problem with many practical variants. LKH is one of the state-of-the-art local search algorithms for the TSP. LKH-3 is a powerful extension of LKH that can solve many TSP variants. Both LKH and LKH-3 associate a candidate set to each city to improve the efficiency, and have two different methods, $\alpha$-measure and POPMUSIC, to decide the candidate sets. In this work, we first propose a Variable Strategy Reinforced LKH (VSR-LKH) algorithm, which incorporates three reinforcement learning methods (Q-learning, Sarsa, Monte Carlo) with LKH, for the TSP. We further propose a new algorithm called VSR-LKH-3 that combines the variable strategy reinforcement learning method with LKH-3 for typical TSP variants, including the TSP with time windows (TSPTW) and Colored TSP (CTSP). The proposed algorithms replace the inflexible traversal operations in LKH and LKH-3 and let the algorithms learn to make a choice at each search step by reinforcement learning. Both LKH and LKH-3, with either $\alpha$-measure or POPMUSIC, can be significantly improved by our methods. Extensive experiments on 236 widely-used TSP benchmarks with up to 85,900 cities demonstrate the excellent performance of VSR-LKH. VSR-LKH-3 also significantly outperforms the state-of-the-art heuristics for TSPTW and CTSP.
翻译:TSP 是一个古老的NP- 硬组合组合优化问题, 有许多实用的变体。 LKH 是TSP 最先进的本地搜索算法之一。 LKH-3 是LKH 的强大扩展, 能够解决许多 TSP 变体。 LKH 和 LKH-3 将一个候选人组合与每个城市联系起来, 以提高效率, 并有两种不同的方法, 包括用时间窗口( TSPTPTW) 和有色TSP (CCTSP) 来决定候选人组。 在这项工作中, 我们首先提出一个变数战略强化的LKH (VSR- LKH) 算法, 其中包括三种最先进的LKSP( VSR- C- CSB) 和 LKK-3 算法, 并且通过LK- KMAL 和 LK 校程的LML 学习率, 也可以通过LK- SLML 和LML 学习一个显著的变数。