Approximation capability of two hidden layer feedforward neural networks with fixed weights

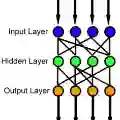
We algorithmically construct a two hidden layer feedforward neural network (TLFN) model with the weights fixed as the unit coordinate vectors of the $d$-dimensional Euclidean space and having $3d+2$ number of hidden neurons in total, which can approximate any continuous $d$-variable function with an arbitrary precision. This result, in particular, shows an advantage of the TLFN model over the single hidden layer feedforward neural network (SLFN) model, since SLFNs with fixed weights do not have the capability of approximating multivariate functions.