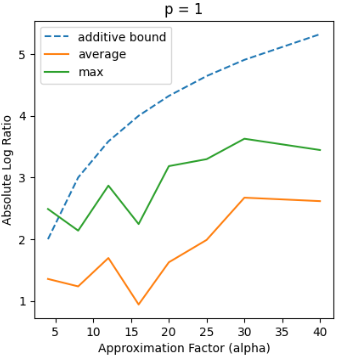
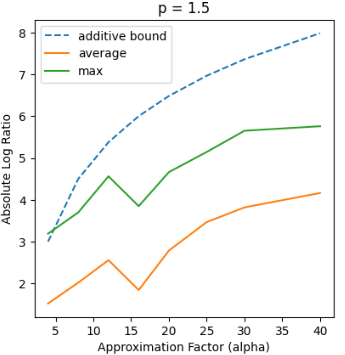
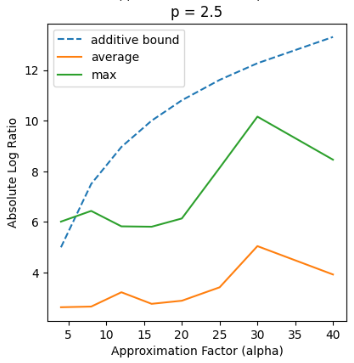
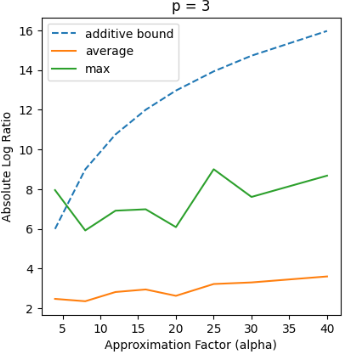
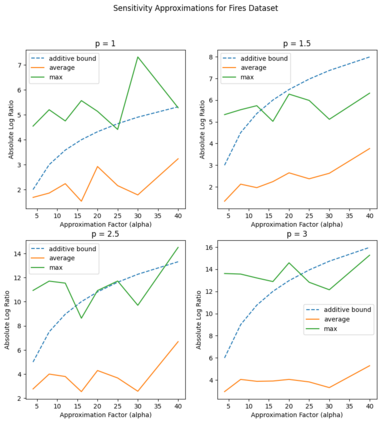
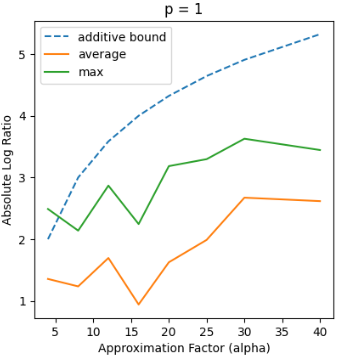
Recent works in dimensionality reduction for regression tasks have introduced the notion of sensitivity, an estimate of the importance of a specific datapoint in a dataset, offering provable guarantees on the quality of the approximation after removing low-sensitivity datapoints via subsampling. However, fast algorithms for approximating $\ell_p$ sensitivities, which we show is equivalent to approximate $\ell_p$ regression, are known for only the $\ell_2$ setting, in which they are termed leverage scores. In this work, we provide efficient algorithms for approximating $\ell_p$ sensitivities and related summary statistics of a given matrix. In particular, for a given $n \times d$ matrix, we compute $\alpha$-approximation to its $\ell_1$ sensitivities at the cost of $O(n/\alpha)$ sensitivity computations. For estimating the total $\ell_p$ sensitivity (i.e. the sum of $\ell_p$ sensitivities), we provide an algorithm based on importance sampling of $\ell_p$ Lewis weights, which computes a constant factor approximation to the total sensitivity at the cost of roughly $O(\sqrt{d})$ sensitivity computations. Furthermore, we estimate the maximum $\ell_1$ sensitivity, up to a $\sqrt{d}$ factor, using $O(d)$ sensitivity computations. We generalize all these results to $\ell_p$ norms for $p > 1$. Lastly, we experimentally show that for a wide class of matrices in real-world datasets, the total sensitivity can be quickly approximated and is significantly smaller than the theoretical prediction, demonstrating that real-world datasets have low intrinsic effective dimensionality.
翻译:暂无翻译