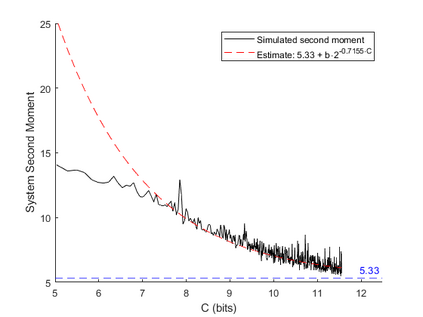
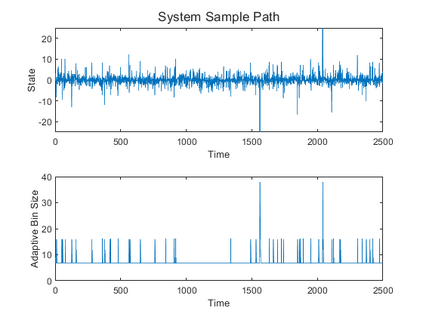
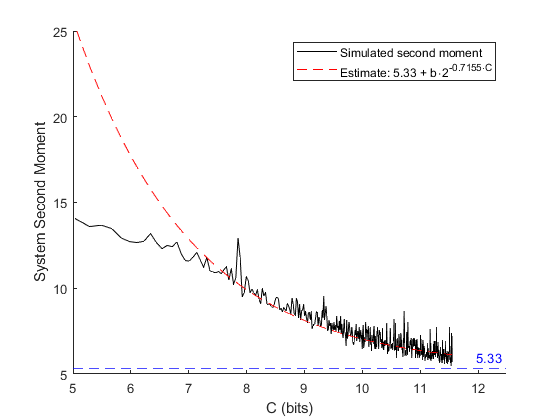
It is known that under fixed-rate information constraints, adaptive quantizers can be used to stabilize an open-loop-unstable linear system on $\mathbb{R}^n$ driven by unbounded noise. These adaptive schemes can be designed so that they have near-optimal rate, and the resulting system will be stable in the sense of having an invariant probability measure, or ergodicity, as well as boundedness of the state second moment. Although structural results and information theoretic bounds of encoders have been studied, the performance of such adaptive fixed-rate quantizers beyond stabilization has not been addressed. In this paper, we propose a two-part adaptive (fixed-rate) coding scheme that achieves state second moment convergence to the classical optimum (i.e., for the fully observed setting) under mild moment conditions on the noise process. The first part, as in prior work, leads to ergodicity (via positive Harris recurrence) and the second part ensures that the state second moment converges to the classical optimum at high rates. These results are established using an intricate analysis which uses random-time state-dependent Lyapunov stochastic drift criteria as a core tool.
翻译:众所周知,在固定利率信息限制下,可使用适应性量子来稳定以无限制噪音驱动的美元驱动的开放环状线性线性系统。这些适应性量子可以设计成接近最佳率的两部分适应性(固定率)编码方案,由此形成的系统在噪音过程的温和条件下(即完全观察到的环境),在不易变概率衡量或偏差的意义上是稳定的,以及国家第二时刻的界限。虽然已经研究了编码器的结构结果和信息理论界限,但这种非稳定化的适应性固定率量子的性能尚未得到解决。在本文中,我们建议采用两部分适应性(固定率)编码方案,在噪音过程的温和条件下,实现与典型最佳水平(即完全观察到的环境)的第二次趋同状态。第一部分与先前的工作一样,导致偏差(通过正数哈里斯的复发)和第二部分确保状态第二点与古典最佳利率相近于高速率的状态。这些结果是使用一个复杂的核心性分析工具,使用随机的流式工具。