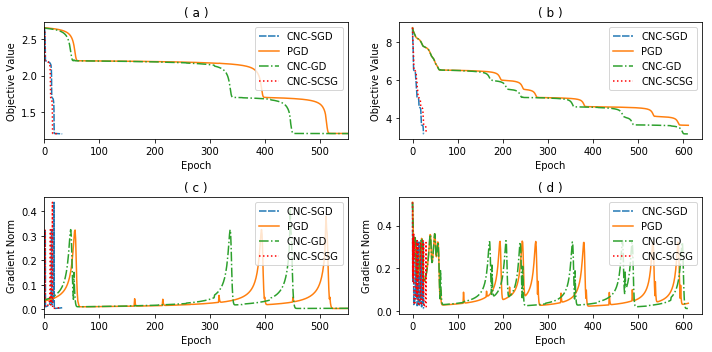
Stochastically controlled stochastic gradient (SCSG) methods have been proved to converge efficiently to first-order stationary points which, however, can be saddle points in nonconvex optimization. It has been observed that a stochastic gradient descent (SGD) step introduces anistropic noise around saddle points for deep learning and non-convex half space learning problems, which indicates that SGD satisfies the correlated negative curvature (CNC) condition for these problems. Therefore, we propose to use a separate SGD step to help the SCSG method escape from strict saddle points, resulting in the CNC-SCSG method. The SGD step plays a role similar to noise injection but is more stable. We prove that the resultant algorithm converges to a second-order stationary point with a convergence rate of $\tilde{O}( \epsilon^{-2} log( 1/\epsilon))$ where $\epsilon$ is the pre-specified error tolerance. This convergence rate is independent of the problem dimension, and is faster than that of CNC-SGD. A more general framework is further designed to incorporate the proposed CNC-SCSG into any first-order method for the method to escape saddle points. Simulation studies illustrate that the proposed algorithm can escape saddle points in much fewer epochs than the gradient descent methods perturbed by either noise injection or a SGD step.
翻译:已经证明,对沙丘控制的沙丘梯度(SCSG)方法能够有效地与一阶固定点相趋同,然而,这些固定点可能是非电流优化的支撑点,据观察,一个随机梯度梯度梯度梯度梯度(SGD)步骤在马鞍点周围造成厌食性噪音,造成深层学习和非电流半空学习问题,这表明SGD满足了与这些问题相关的负曲线(CNC)条件。因此,我们提议采用单独的SGD步骤,帮助SCGD方法从严格的马鞍点逃出,从而形成CNC-SC-SCG方法。SGD步骤的作用类似于噪音注入,但更稳定。我们证明,一个结果的算法将二阶固定点趋同到第二阶点,其趋同率为$tilde{O}(\epsilon ⁇ -2}log (1/\epsilon)),其中美元是预先确定的错误容忍度。我们提议采用这种趋同率与问题层面无关,而且比CNC-SG-SG方法第一步更快。一个较一般的框架用于Smarelma 方向的越轨方法。