Variational integrators for non-autonomous systems with applications to stabilization of multi-agent formations

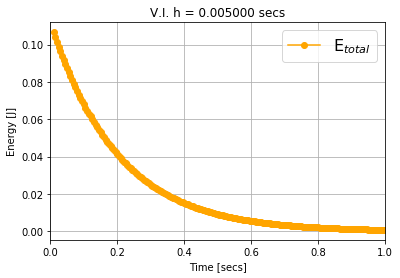
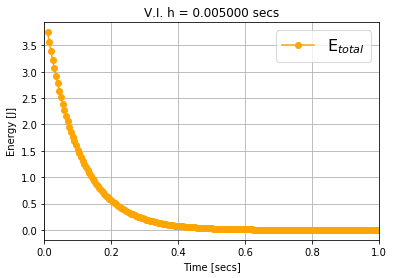
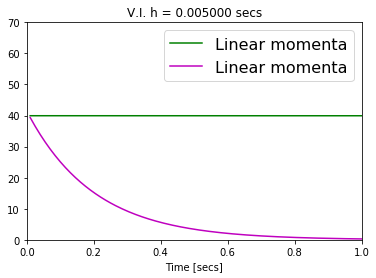
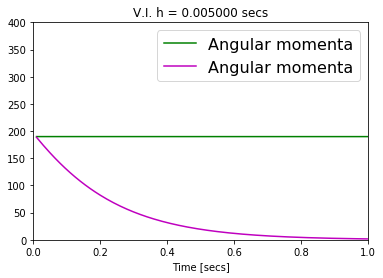
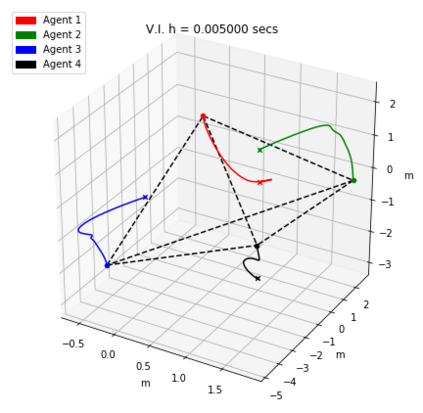
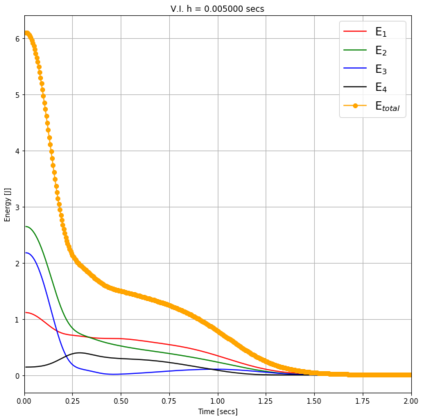
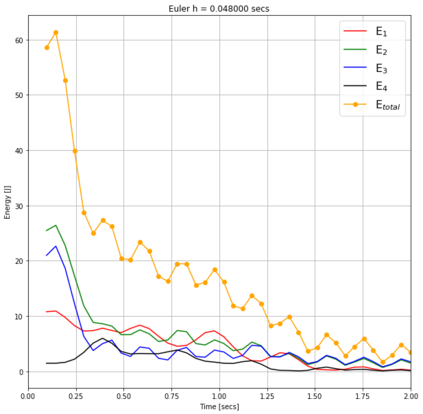
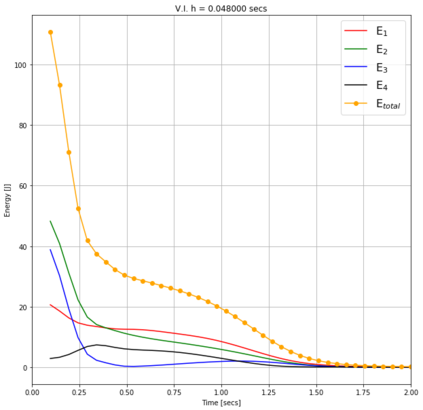
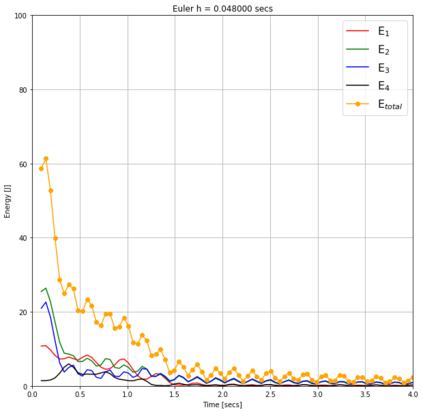
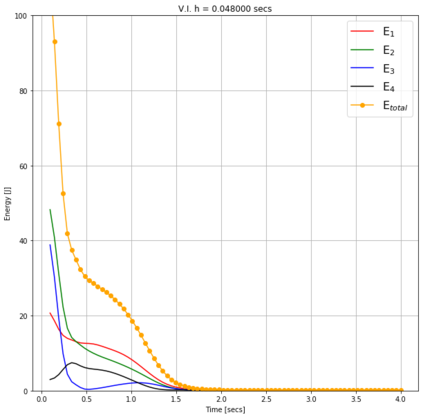
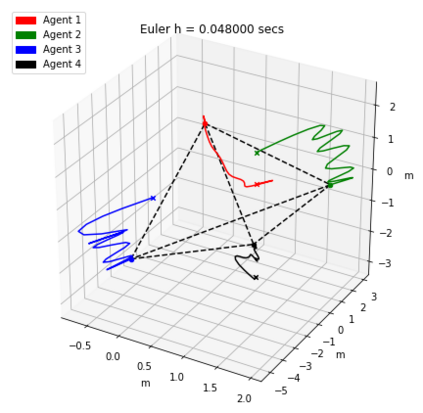
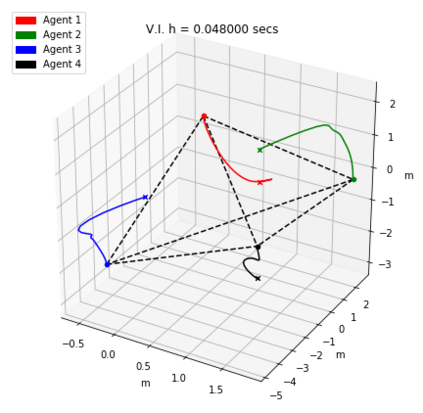
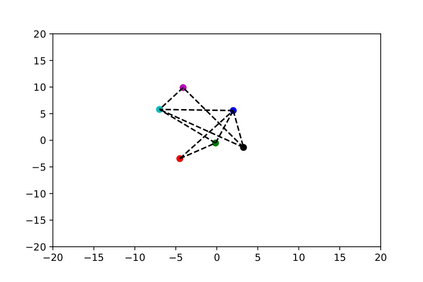
Numerical methods that preserve geometric invariants of the system, such as energy, momentum or the symplectic form, are called geometric integrators. Variational integrators are an important class of geometric integrators. The general idea for those variational integrators is to discretize Hamilton's principle rather than the equations of motion in a way that preserves some of the invariants of the original system. In this paper we construct variational integrators with fixed time step for time-dependent Lagrangian systems modelling an important class of autonomous dissipative systems. These integrators are derived via a family of discrete Lagrangian functions each one for a fixed time-step. This allows to recover at each step on the set of discrete sequences the preservation properties of variational integrators for autonomous Lagrangian systems, such as symplecticity or backward error analysis for these systems. We also present a discrete Noether theorem for this class of systems. Applications of the results are shown for the problem of formation stabilization of multi-agent systems.