Linearity Characterization and Uncertainty Quantification of Spectroradiometers via Maximum Likelihood and the Non-parametric Bootstrap

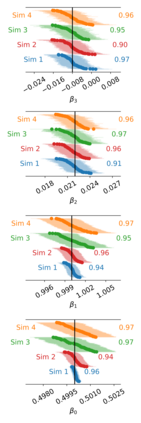
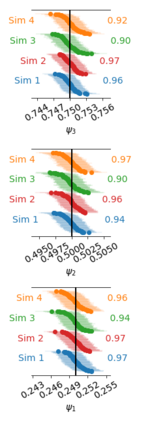
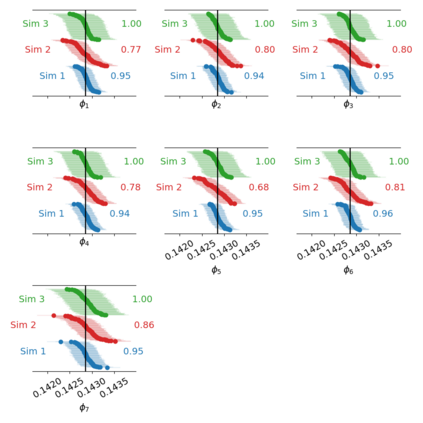
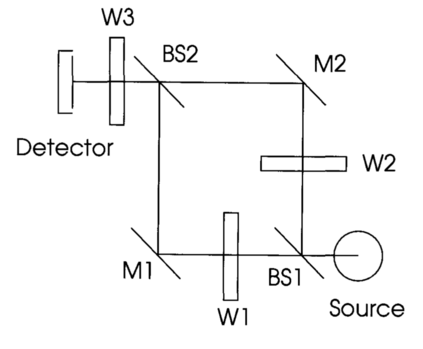
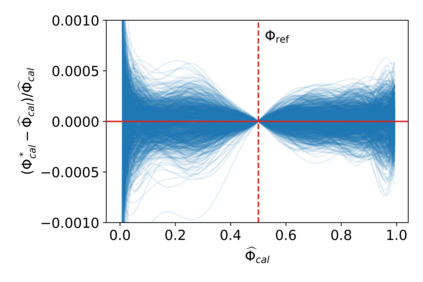
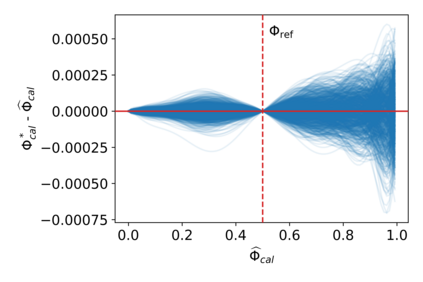
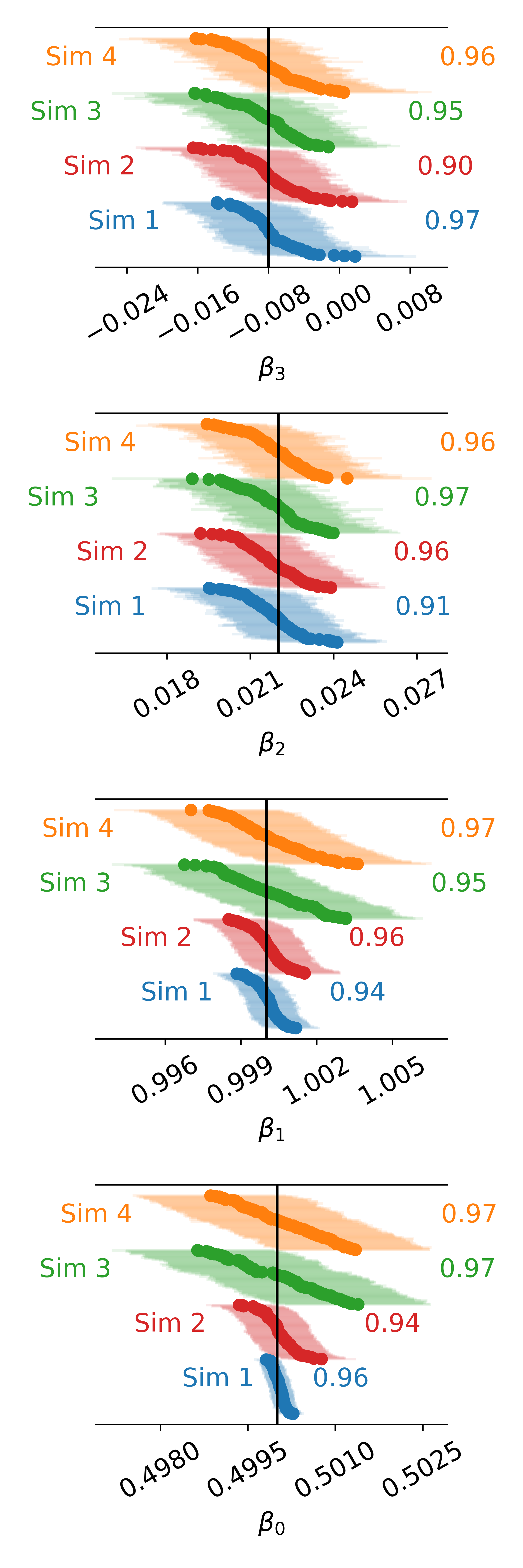
A rigorous uncertainty quantification for "flux-addition," (also known as the "combinatoric technique") a well-known technique in the radiometry field, is investigated. A probabilistic model for digital readings at given fluxes and values of polynomial coefficients describing the nonlinear instrument response is proposed. Maximum likelihood estimates (MLEs) of the unknown fluxes and polynomial coefficients are recommended. A non-parametric bootstrap algorithm is introduced to quantify uncertainty, e.g., to calculate standard errors. The model and bootstrap algorithm are studied by simulation. These simulation are performed using fluxes and polynomial coefficients consistent with those observed during the characterization of the Orbiting Carbon Observatory-2, for each of its focal planes. The MLEs are found to be approximately unbiased, and confidence intervals derived from the bootstrap replicates are found to be consistent with their target coverage of 95 %. For the polynomial coefficients representing the linearization function, the relative bias was less than 1 % and the observed coverages range from 90 % to 97 %. An experimental data set from the NIST Beam Conjoiner, which implements flux addition with a broadband light-source and a set of neutral density filters, is also considered. In this example, a complete calibration is generated assuming that one flux level is well characterized by the spectroradiometer. The uncertainty contribution attributable to estimation of the instrument's nonlinear response is less than 0.02 % over most of its range.