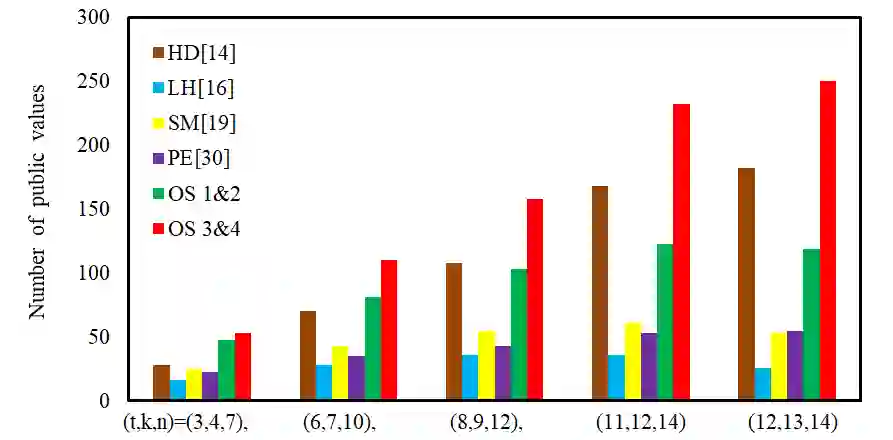
Secret sharing was firstly proposed in 1979 by Shamir and Blakley respectively. To avoid deficiencies of original schemes, researchers presented improvement schemes, among which the multi-secret sharing scheme (MSS) is significant. There are three categories of MSSs, however, we focus on multi-stage secret sharing scheme (MSSS) recovering secrets with any order in this work. By observing inhomogeneous linear recursions (ILRs) in the literature, we conclude a general formula and divide ILRs into two types according to different variables in them. Utilizing these two kinds of ILRs, we propose four verifiable MSSSs with Ajtai's function, which is a lattice-based function. Our schemes have the following advantages. Firstly, our schemes can detect cheat of the dealer and participants, and are multi-use. Secondly, we have several ways to restore secrets. Thirdly, we can turn our schemes into other types of MSSs due to the universality of our method. Fourthly, since we utilize a lattice-based function to mask shares, our schemes can resist the attack from the quantum computer with computational security. Finally, although our schemes need more memory consumption than some known schemes, we need much less time consumption, which makes our schemes more suitable facing limited computing power.
翻译:1979年,Shamir 和 Blakley 分别首次提出秘密共享。 为了避免原始计划的缺陷,研究人员提出了改进计划,其中多保密共享计划很重要。 但是,我们侧重于三类多阶段秘密共享计划,以任何顺序恢复秘密。 通过观察文献中的不相容线性循环(ILR),我们得出了一种通用公式,并将ILR分为两种不同的变量。 利用这两种ILRS,我们提出了四种具有Ajtai功能的可核实MSSS(MSS)改进计划,这是一个基于套装功能的功能。我们的计划有以下优点:首先,我们的计划可以发现交易者和参与者的欺骗,并且具有多种用途。第二,我们可以通过观察不同种类的线性线性循环(ILRs)来恢复秘密。 第三,我们可以根据我们的方法的普遍性,将我们的计划变成其他类型的MSS。 第四,由于我们利用一种基于套装功能来掩盖共享,我们的一些计划可以抵御量子计算机的攻击,而Ajtai的功能则是基于套装功能。 我们的计划有以下的优点。 首先,我们的计划可以发现对交易商和参与者的偏差的消费计划。 最后,我们需要比我们的计算方法要少一些时间。