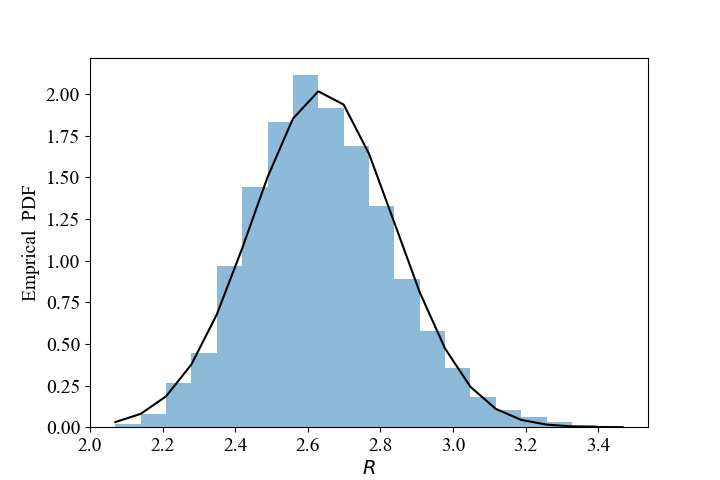
Faster-than-Nyquist (FTN) signaling is a candidate non-orthonormal transmission technique to improve the spectral efficiency (SE) of future communication systems. However, such improvements of the SE are at the cost of additional computational complexity to remove the intentionally introduced intersymbol interference. In this paper, we investigate the use of deep learning (DL) to reduce the detection complexity of FTN signaling. To eliminate the need of having a noise whitening filter at the receiver, we first present an equivalent FTN signaling model based on using a set of orthonormal basis functions and identify its operation region. Second, we propose a DL-based list sphere decoding (DL-LSD) algorithm that selects and updates the initial radius of the original LSD to guarantee a pre-defined number $N_{\text{L}}$ of lattice points inside the hypersphere. This is achieved by training a neural network to output an approximate initial radius that includes $N_{\text{L}}$ lattice points. At the testing phase, if the hypersphere has more than $N_{\text{L}}$ lattice points, we keep the $N_{\text{L}}$ closest points to the point corresponding to the received FTN signal; however, if the hypersphere has less than $N_{\text{L}}$ points, we increase the approximate initial radius by a value that depends on the standard deviation of the distribution of the output radii from the training phase. Then, the approximate value of the log-likelihood ratio (LLR) is calculated based on the obtained $N_{\text{L}}$ points. Simulation results show that the computational complexity of the proposed DL-LSD is lower than its counterpart of the original LSD by orders of magnitude.
翻译:高于 Nyquist (FTN) 的快速超快信号是用于提高未来通信系统的光谱效率( SE) 的候选非异常传输技术。 然而, SE 的这种改进是以额外的计算复杂性为代价的, 以删除有意引入的跨符号干扰。 在本文中, 我们调查深度学习( DL) 的使用情况, 以降低 FTN 信号的检测复杂性。 为了消除接收器使用噪声白过滤过滤器的需要, 我们首先推出一个等效的 FTN 信号模型, 以使用一套正态函数函数计算, 并识别其运行区域。 其次, 我们提议基于 DL 的列表域域解码( DL- LSD) 的算法, 选择并更新原始 LSD的初始半径, 以保证预定义的 $N{ text{L} 值 的值。 这是通过训练神经网络输出一个大约初始半径的半径, 包括 $N ⁇ text {L = lix sdemode, laticelex sad lex 。