On exact computation of Tukey depth central regions

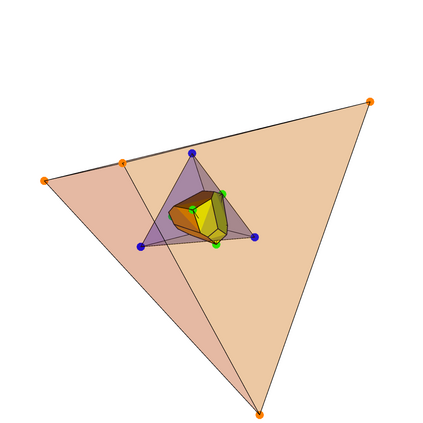
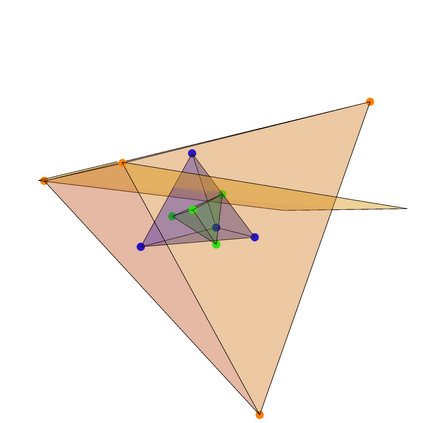
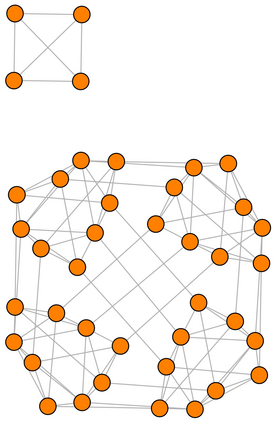
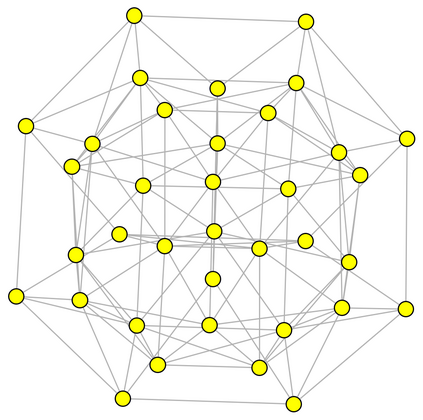
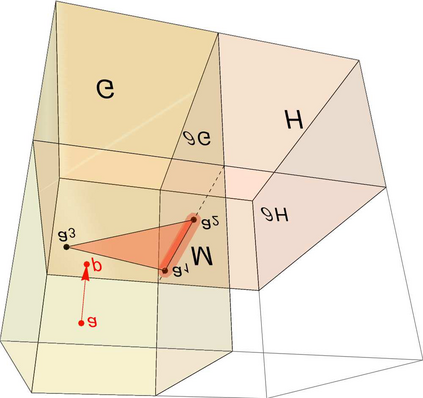
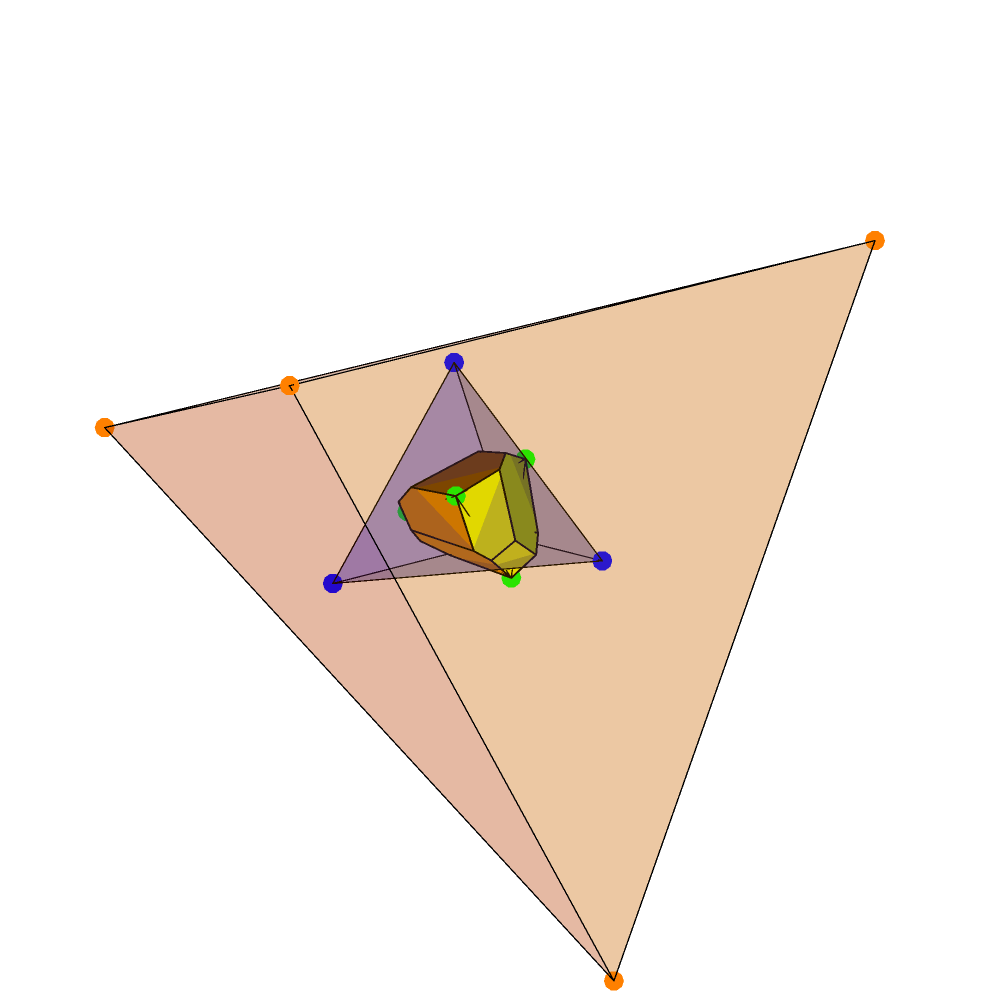
The Tukey (or halfspace) depth extends nonparametric methods toward multivariate data. The multivariate analogues of the quantiles are the central regions of the Tukey depth, defined as sets of points in the $d$-dimensional space whose Tukey depth exceeds given thresholds $k$. We address the problem of fast and exact computation of those central regions. First, we analyse an efficient Algorithm A from Liu et al. (2019), and prove that it yields exact results in dimension $d=2$, or for a low threshold $k$ in arbitrary dimension. We provide examples where Algorithm A fails to recover the exact Tukey depth region for $d>2$, and propose a modification that is guaranteed to be exact. We express the problem of computing the exact central region in its dual formulation, and use that viewpoint to demonstrate that further substantial improvements to our algorithm are unlikely. An efficient C++ implementation of our exact algorithm is freely available in the R package TukeyRegion.