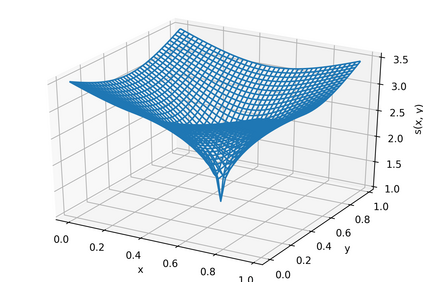
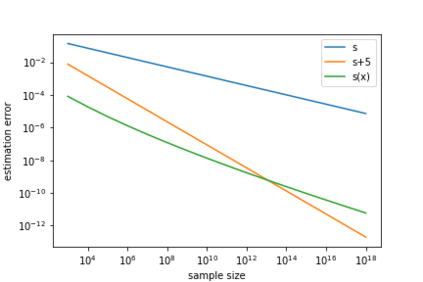
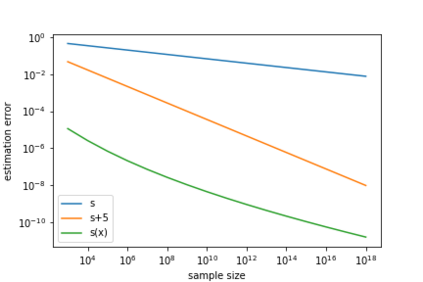
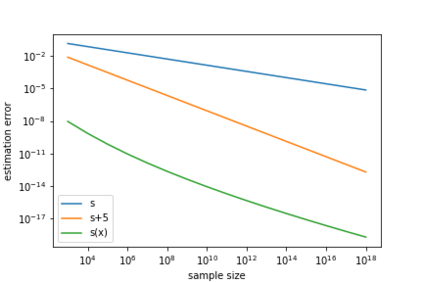
Deep learning has achieved notable success in various fields, including image and speech recognition. One of the factors in the successful performance of deep learning is its high feature extraction ability. In this study, we focus on the adaptivity of deep learning; consequently, we treat the variable exponent Besov space, which has a different smoothness depending on the input location $x$. In other words, the difficulty of the estimation is not uniform within the domain. We analyze the general approximation error of the variable exponent Besov space and the approximation and estimation errors of deep learning. We note that the improvement based on adaptivity is remarkable when the region upon which the target function has less smoothness is small and the dimension is large. Moreover, the superiority to linear estimators is shown with respect to the convergence rate of the estimation error.
翻译:深层学习在各个领域取得了显著成功,包括图像和语音识别。深层学习成功表现的一个因素是其高特征提取能力。在本研究中,我们注重深层学习的适应性;因此,我们处理可变Expentent Besov空间,该空间的平滑性取决于输入地点x美元。换句话说,估算的困难在域内并不一致。我们分析了可变Exponent Besov空间的总体近似误差以及深层学习的近似和估计误差。我们注意到,在目标功能不太平滑且规模较大的区域,基于适应性的改进是显著的。此外,在估算误差的趋同率方面,线性估计的优越性表现在线性估计误差的趋同率上。