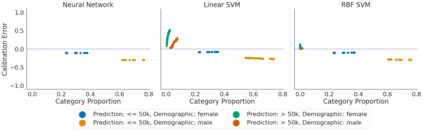
Recent works have investigated the sample complexity necessary for fair machine learning. The most advanced of such sample complexity bounds are developed by analyzing multicalibration uniform convergence for a given predictor class. We present a framework which yields multicalibration error uniform convergence bounds by reparametrizing sample complexities for Empirical Risk Minimization (ERM) learning. From this framework, we demonstrate that multicalibration error exhibits dependence on the classifier architecture as well as the underlying data distribution. We perform an experimental evaluation to investigate the behavior of multicalibration error for different families of classifiers. We compare the results of this evaluation to multicalibration error concentration bounds. Our investigation provides additional perspective on both algorithmic fairness and multicalibration error convergence bounds. Given the prevalence of ERM sample complexity bounds, our proposed framework enables machine learning practitioners to easily understand the convergence behavior of multicalibration error for a myriad of classifier architectures.
翻译:最近的工作调查了公平机器学习所需的样本复杂性。 最先进的样本复杂性界限是通过分析某一预测值类的多校准统一趋同度来开发的。 我们提出了一个框架,通过重新校正经验风险最小化(ERM)学习的样本复杂性来产生多校正错误统一趋同度界限。 我们从这个框架可以看出,多校正错误证明了对分类结构以及基本数据分布的依赖性。 我们进行了实验性评估,以调查分类者不同家族的多校正错误行为。 我们将这次评估的结果与多校正错误集中界限进行比较。 我们的调查为算法公正和多校正错误趋同度界限提供了更多视角。 鉴于机构抽样复杂性的普遍存在,我们提议的框架使机器学习实践者能够轻松理解多种分类师结构的多校正错误的趋同性。