The Combinatorics of Motzkin Polyominoes

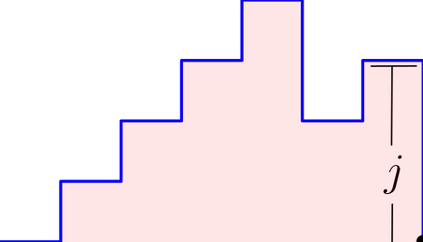
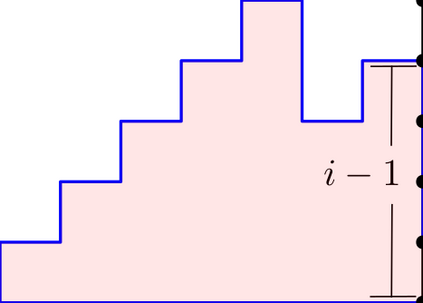
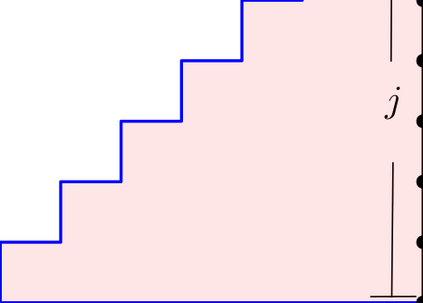
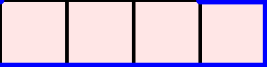
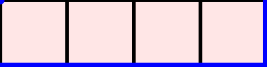
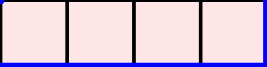
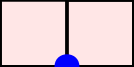
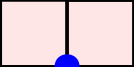
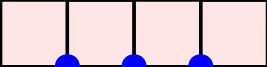
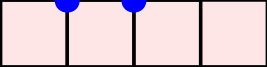
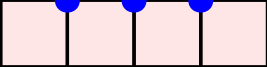
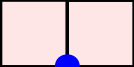
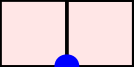
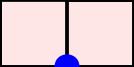
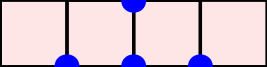
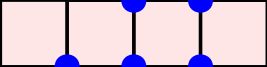
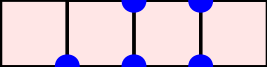
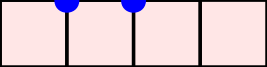
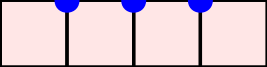
A word $w=w_1\cdots w_n$ over the set of positive integers is a Motzkin word whenever $w_1=\texttt{1}$, $1\leq w_k\leq w_{k-1}+1$, and $w_{k-1}\neq w_{k}$ for $k=2, \dots, n$. It can be associated to a $n$-column Motzkin polyomino whose $i$-th column contains $w_i$ cells, and all columns are bottom-justified. We reveal bijective connections between Motzkin paths, restricted Catalan words, primitive {\L}ukasiewicz paths, and Motzkin polyominoes. Using the aforementioned bijections together with classical one-to-one correspondence with Dyck paths avoiding $UDU$s, we provide generating functions with respect to the length, area, semiperimeter, value of the last symbol, and number of interior points of Motzkin polyominoes. We give asymptotics and close expressions for the total area, total semiperimeter, sum of the last symbol values, and total number of interior points over all Motzkin polyominoes of a given length. We also present and prove an engaging trinomial relation concerning the number of cells lying at different levels and first terms of the expanded $(1+x+x^2)^n$.