Local error quantification for Neural Network Differential Equation solvers

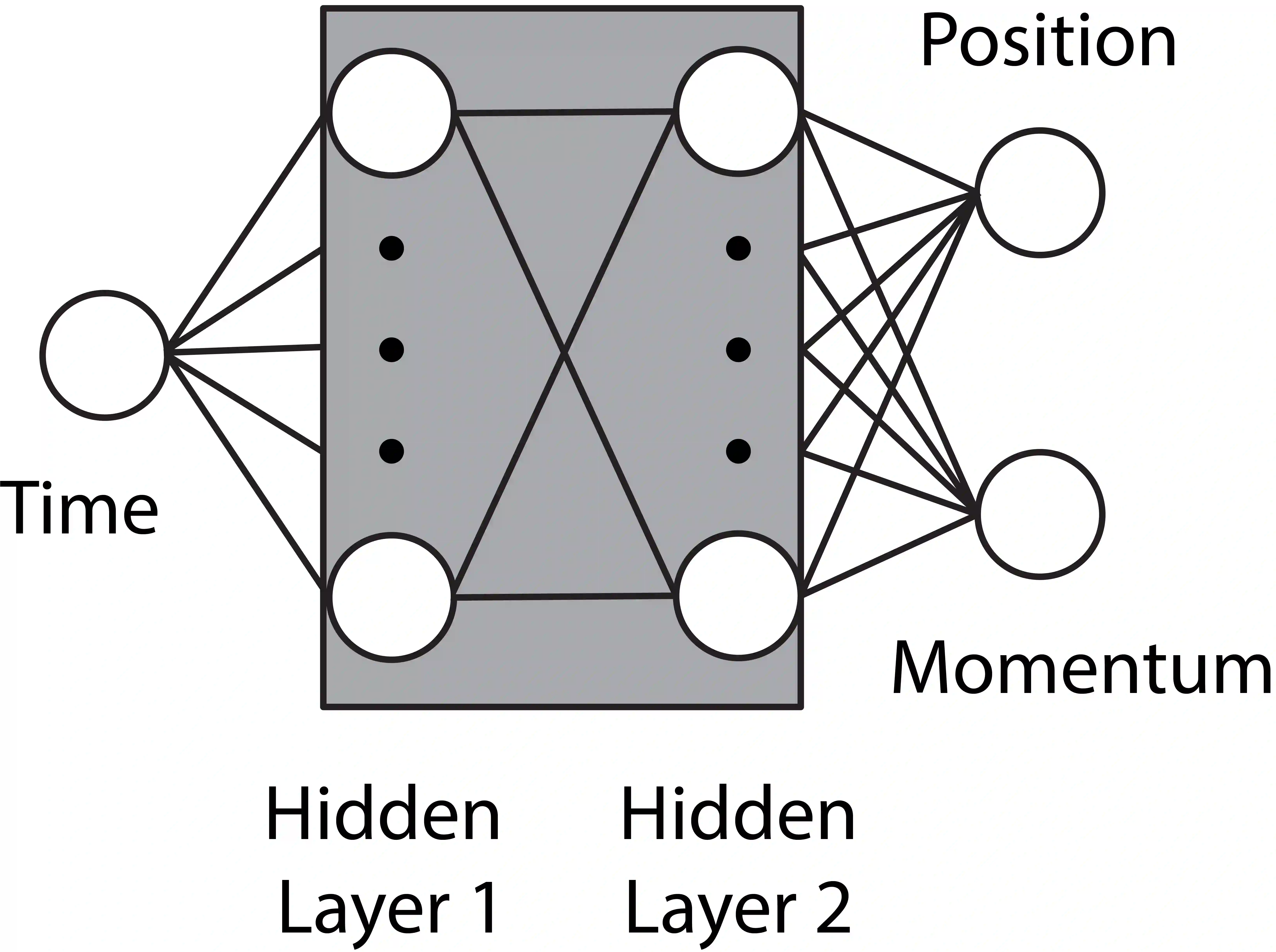
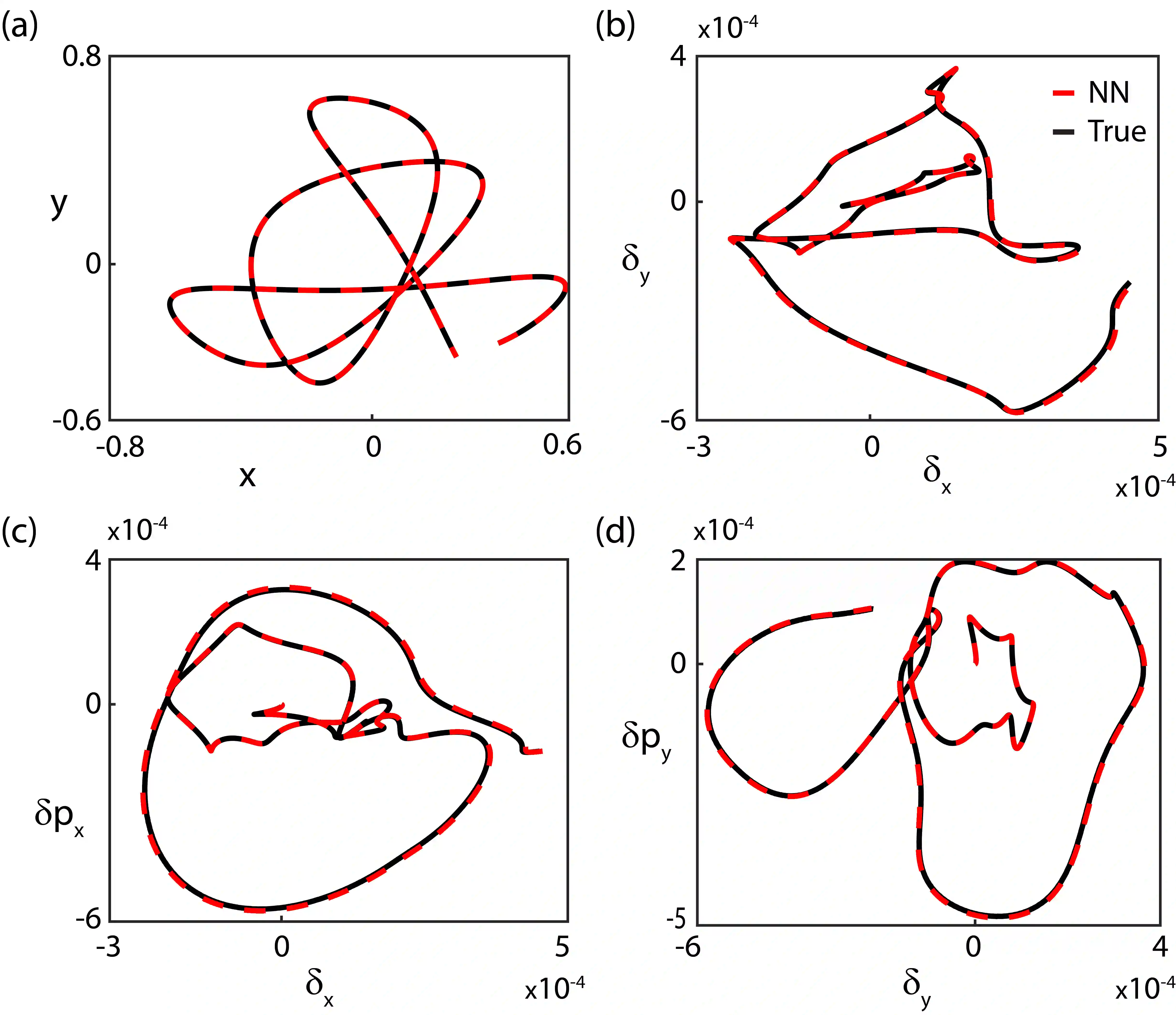
Neural networks have been identified as powerful tools for the study of complex systems. A noteworthy example is the neural network differential equation (NN DE) solver, which can provide functional approximations to the solutions of a wide variety of differential equations. Such solvers produce robust functional expressions, are well suited for further manipulations on the quantities of interest (for example, taking derivatives), and capable of leveraging the modern advances in parallelization and computing power. However, there is a lack of work on the role precise error quantification can play in their predictions: usually, the focus is on ambiguous and/or global measures of performance like the loss function and/or obtaining global bounds on the errors associated with the predictions. Precise, local error quantification is seldom possible without external means or outright knowledge of the true solution. We address these concerns in the context of dynamical system NN DE solvers, leveraging learnt information within the NN DE solvers to develop methods that allow them to be more accurate and efficient, while still pursuing an unsupervised approach that does not rely on external tools or data. We achieve this via methods that can precisely estimate NN DE solver prediction errors point-wise, thus allowing the user the capacity for efficient and targeted error correction. We exemplify the utility of our methods by testing them on a nonlinear and a chaotic system each.