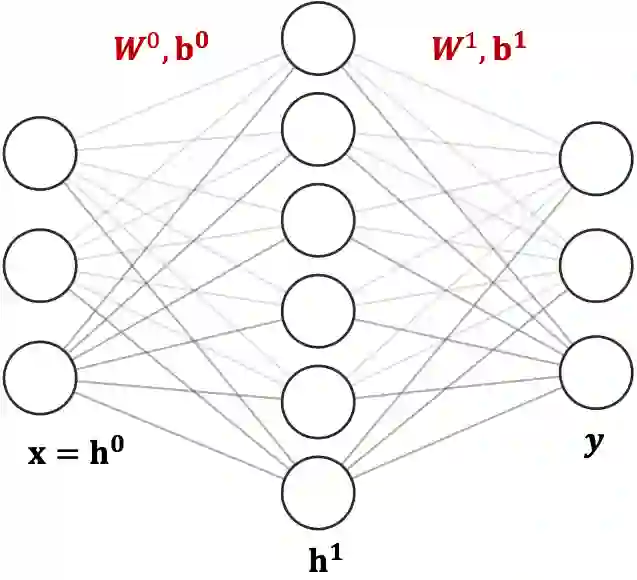
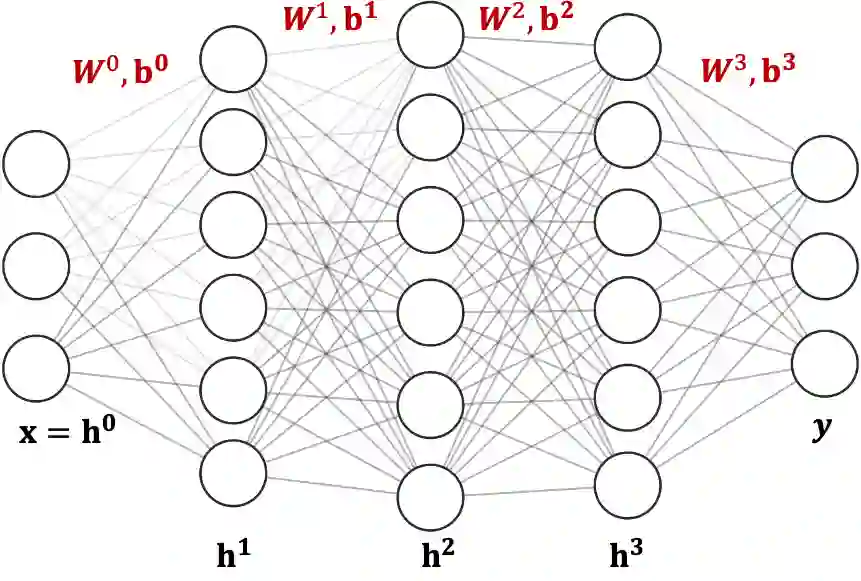
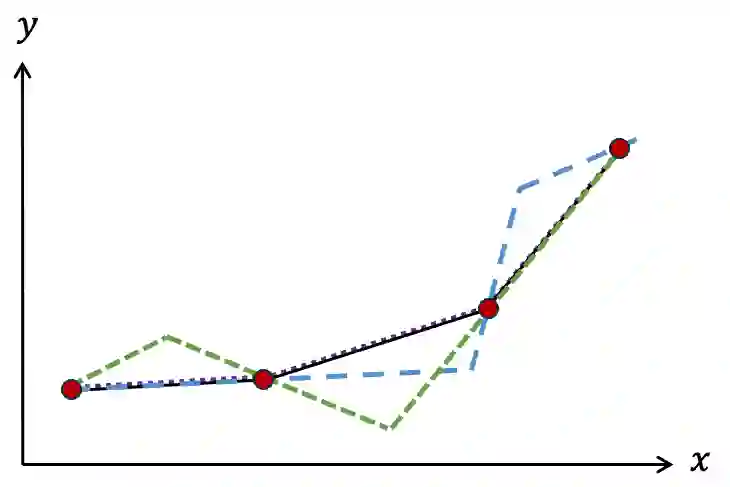
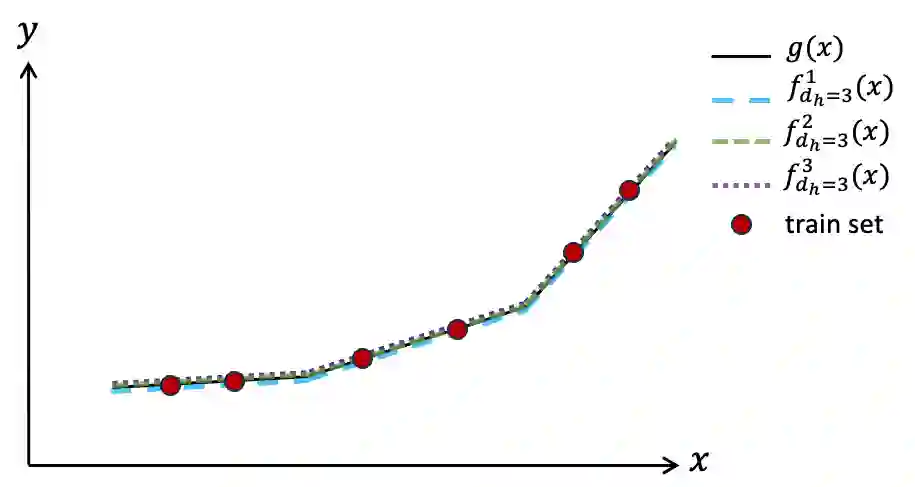
Neural Networks (NN) with ReLU activation functions are used to model multiparametric quadratic optimization problems (mp-QP) in diverse engineering applications. Researchers have suggested leveraging the piecewise affine property of deep NN models to solve mp-QP with linear constraints, which also exhibit piecewise affine behaviour. However, traditional deep NN applications to mp-QP fall short of providing optimal and feasible predictions, even when trained on large datasets. This study proposes a partially-supervised NN (PSNN) architecture that directly represents the mathematical structure of the global solution function. In contrast to generic NN training approaches, the proposed PSNN method derives a large proportion of model weights directly from the mathematical properties of the optimization problem, producing more accurate solutions despite significantly smaller training data sets. Many energy management problems are formulated as QP, so we apply the proposed approach to energy systems (specifically DC optimal power flow) to demonstrate proof of concept. Model performance in terms of solution accuracy and speed of predictions was compared against a commercial solver and a generic Deep NN model based on classical training. Results show KKT sufficient conditions for PSNN consistently outperform generic NN architectures with classical training using far less data, including when tested on extreme, out-of-training distribution test data. Given its speed advantages over traditional solvers, the PSNN model can quickly produce optimal and feasible solutions within a second for millions of input parameters sampled from a distribution of stochastic demands and renewable generator dispatches, which can be used for simulations and long term planning.
翻译:具有ReLU激活函数的神经网络被广泛应用于各类工程应用中的多参数二次优化问题建模。研究者提出利用深度神经网络的分段仿射特性来求解同样呈现分段仿射行为的线性约束多参数二次规划问题。然而,传统深度神经网络应用于多参数二次规划时,即使在大型数据集上训练,仍难以提供最优且可行的预测。本研究提出一种部分监督神经网络架构,直接表征全局解函数的数学结构。与通用神经网络训练方法相比,所提出的PSNN方法直接从优化问题的数学特性推导出大部分模型权重,从而在训练数据集显著更小的情况下获得更精确的解。由于众多能源管理问题可表述为二次规划,我们将该方法应用于能源系统(特别是直流最优潮流)以验证概念可行性。在解精度和预测速度方面,将模型性能与商业求解器及基于经典训练的通用深度神经网络模型进行比较。结果表明:在数据量极少的情况下,PSNN的KKT充分条件始终优于采用经典训练的通用神经网络架构,即使在极端、超出训练分布的测试数据上也是如此。鉴于其相对于传统求解器的速度优势,PSNN模型可在1秒内为从随机需求与可再生能源机组出力的分布中采样的数百万输入参数快速生成最优可行解,这可用于系统仿真与长期规划。