Data Mapping for Restricted Boltzmann Machine

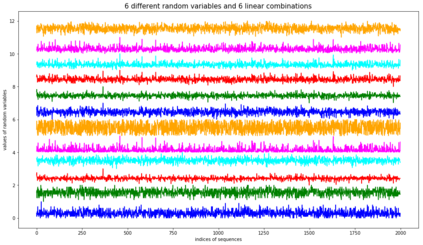
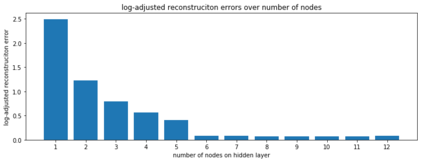
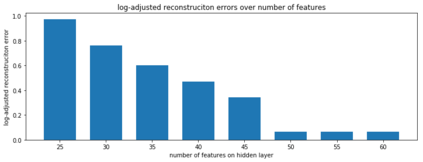
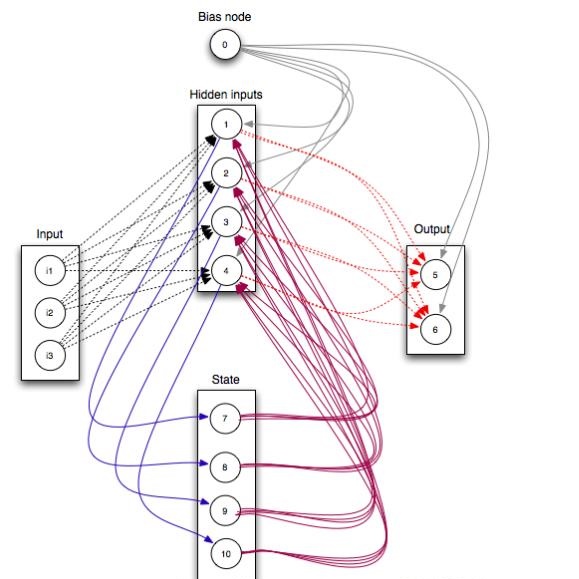
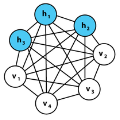
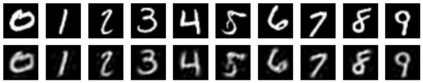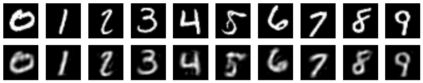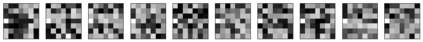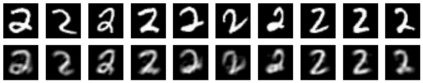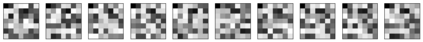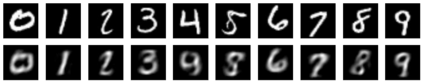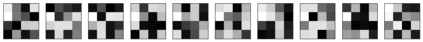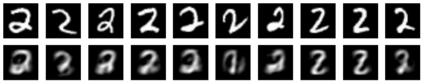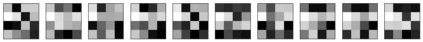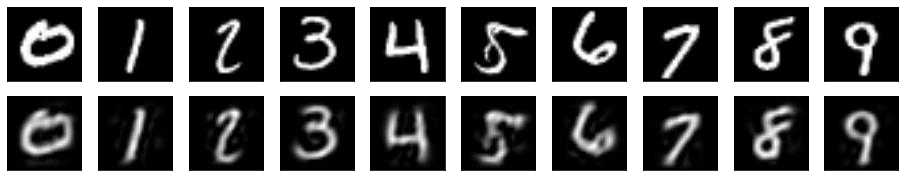Restricted Boltzmann machine (RBM) is interpreted as a data mapping between visible and hidden layers without using the energy function. The idea of data mapping is to let the visible layer reconstruct the hidden layer in terms of minimizing a squared error to replace the probabilistic model of maximizing a product of probabilities. With the data mapping framework, this paper presents three new findings: 1) data on visible and hidden layers can be real-valued matrix data; 2) contrastive divergence is a finite difference approximation of the gradient descent and can be applied to train the directed graph as well; 3) activation can be non-sigmoid functions, for example, identity, relu and softsign. The reinterpreted RBM provides a general framework on dimensionality reduction, feature extraction and data representation pioneered and developed by Hinton and his colleagues. Numerical results are included to demonstrate the feasibility of data mapping on very low dimensionality reduction, matrix data and flexible activation.